In Analisi Matematica ci è sicuramente capitato di avere a che fare con funzioni del tipo:
\begin{equation} \begin{split} f\colon & A (\subseteq \R ) \\ & x \rightarrow y=f(x) \end{split} \end{equation}Una funzione di questo tipo prende in ingresso un input x e restituisce in uscita un output y.
Poiché tale output è un numero, una funzione di questo tipo è detta funzione scalare.
Consideriamo ora funzioni in cui l’output non è più un singolo valore bensì un vettore: tali funzioni vengono definite vettoriali.
Se la dimensione dell’output è 2 o 3, cioè se in uscita otteniamo una coppia o una terna di valori, indichiamo queste funzioni con il termine curve.
Concentriamoci sulle curve nel piano, cioè quelle per cui l’output è costituito da un vettore di due componenti (i ragionamenti si estendono in maniera analoga al caso tridimensionale).
Una curva viene solitamente indicata con la seguente notazione:
\begin{equation} \begin{split} \gamma \colon & [a,b] (\subseteq \R ) \to \R^2 \\ & t \rightarrow (x(t),y(t))=\gamma(t) \end{split} \end{equation} La curva \gamma prende in ingresso l’input t e restituisce in uscita il vettore (x(t),y(t)).
Poiché il grafico di una funzione è dato dall’insieme dei punti le cui coordinate sono le coppie input-output, nel caso delle curve il grafico vive nello spazio (t, x, y).

Piuttosto che il grafico, ciò che ci interessa conoscere di una curva è il suo sostegno, cioè l’immagine della curva nel piano x-y.

Se interpretiamo t come il tempo, il sostegno di una curva può essere interpretato come la traiettoria descritta da un punto materiale che si muove con legge oraria \gamma = \gamma(t) nell’intervallo di tempo [a,b].
Quando studiamo una curva siamo interessati in particolar modo a quattro sue proprietà:
la chiusura, la semplicità, la regolarità e la lunghezza.
Chiusura
Una curva \gamma \colon [a,b] \to \R^2 si dice chiusa se:
\begin{equation}
\gamma(a) = \gamma(b)
\end{equation}cioè se il “punto iniziale della traiettoria coincide con il punto finale”.
Ad esempio, riferendoci ai sostegni che seguono si ha che la prima curva è aperta e la seconda è chiusa.

Osserviamo una cosa.
Osservando il sostegno qui accanto potremmo essere portati a dire che la relativa curva sia chiusa ma non è così: il punto “di partenza” \gamma(a) non coincide con il punto “di arrivo” \gamma(b).

Semplicità
Una curva \gamma \colon [a,b] \to \R^2 si dice semplice se
\begin{equation}
\gamma(t_1) \ \neq \gamma(t_2) \ \ \ \forall t_1,t_2 \in (a,b) \quad \text{con} \ t_1 \neq t_2
\end{equation}La (4) può essere anche essere sostituita con la seguente:
\begin{equation}
\gamma(t_1) = \gamma(t_2) \iff t_1 = t_2 \quad \text{con} \ t_1,t_2 \in (a,b)
\end{equation}Si noti che nelle definizioni su scritte abbiamo escluso gli estremi dell’intervallo di definizione della curva in quanto una curva chiusa può essere semplice.

Dal punto di vista fenomenologico, dire che una curva è semplice equivale a dire che il punto materiale che descrive la traiettoria non passa più di una volta in uno stesso punto.
Regolarità
Una curva \gamma \colon [a,b] \to \R^2 si dice regolare se, detto banalmente, è liscia, cioè se il suo sostegno non presenta spigoli.

Matematicamente tale condizione equivale a dire che il sostegno della curva ammette tangente in ogni punto.
Poiché il vettore tangente alla curva in t è dato da
\gamma'(t) = (x'(t), y'(t))
si ha che una curva è regolare se
\gamma'(t) \neq 0 \ \ \forall t \in (a,b) .
L’esistenza di un vettore tangente implica l’esistenza di un versore tangente (cioè un vettore tangente di lunghezza unitaria) dato da:
\begin{equation}
\begin{split}
\vec{T} & = \frac{\gamma'(t)}{||\gamma'(t)||}= \frac{(x'(t), y'(t)) }{\sqrt{[x'(t)^2]+[y'(t)]^2}} =
\\& = \Bigg(\frac{x'(t)}{\sqrt{[x'(t)^2]+[y'(t)]^2}} , \frac{y'(t) }{\sqrt{[x'(t)^2]+[y'(t)]^2}} \Bigg)^T
\end{split}
\end{equation}Come condizione di regolarità possiamo allora assumere:
\begin{equation}
||\gamma'(t)|| = \sqrt{[x'(t)^2]+[y'(t)]^2} \neq 0 \ \ \forall t\in (a,b).
\end{equation}Ricordando che la derivata di una funzione ci dice come varia l’output quando l’input varia di pochissimo, possiamo dire la il vettore \vec \gamma'(t) rappresenta il vettore velocità istantanea del punto materiale dl momento che esso ci dice come varia la posizione al variare del tempo.
Se \vec \gamma'(t) rappresenta il vettore velocità, ||\vec\gamma'(t)|| rappresenta la velocità istantanea scalare, dal momento che la norma di un vettore ne rappresenta la lunghezza.
Osservazione
Oltre al versore tangente possiamo anche definire un versore normale alla curva in un dato punto.
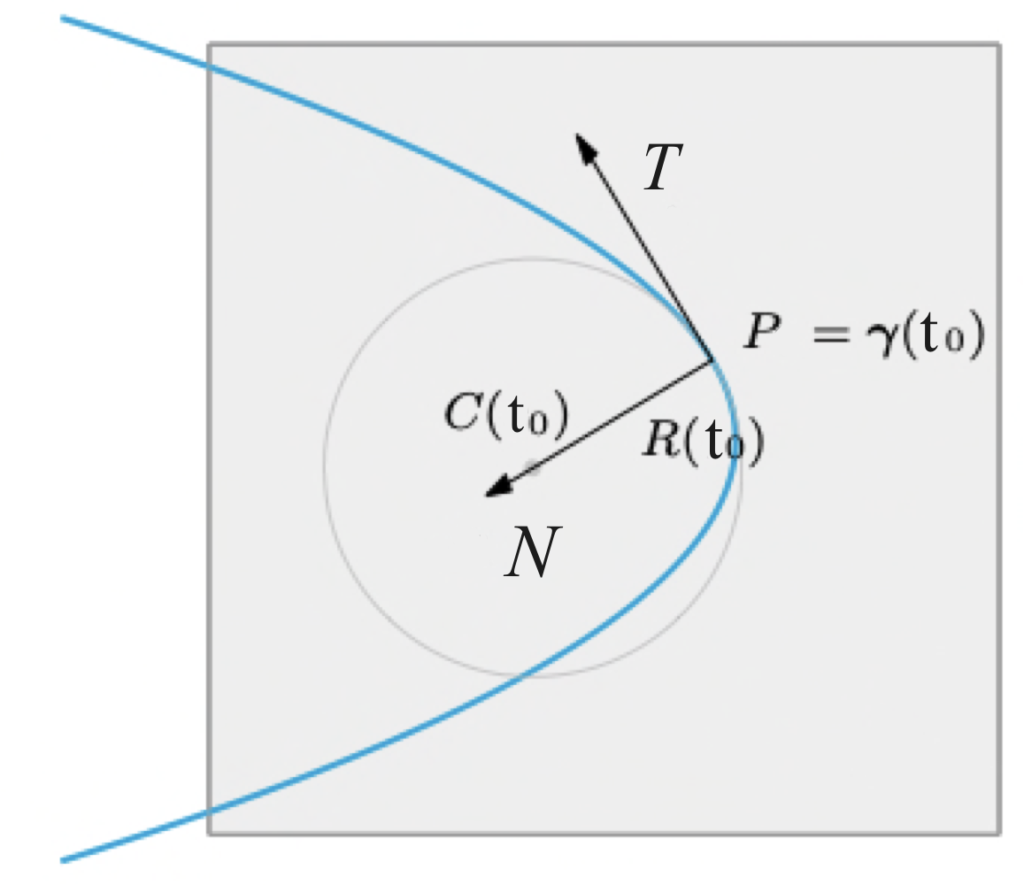
Esso è ortogonale al versore tangente, punta verso il centro di curvatura ed è dato da:
\begin{equation}
\mathbf{N}(t)=\frac{\mathbf{T}'(t)}{||\mathbf{T}'(t)||}
\end{equation}Se \gamma è una curva piana, definiamo curvatura k(t), in un punto t, la quantità {||\mathbf{T}'(t)||}.
Definiamo raggio di curvatura la quantità:
\begin{equation}
R(t)=\frac{1}{k(t)}
\end{equation}Il raggio di curvatura R(t) è il raggio della circonferenza tangente nel punto t al sostegno della curva \gamma(t) che meglio lo approssima localmente. Tale circonferenza è detta circonferenza osculatrice.
Il versore normale e il versore tangente a una curva individuano un piano detto piano osculatore.

Il versore normale a tale piano è detto versore binormale ed è dato da
\begin{equation}
\mathbf B(t)=\mathbf T(t)\times \mathbf N(t)
\end{equation}Osservazione: il versore normale è orientato verso il centro di curvatura e misura quanto la curva differisce da una linea retta.