I video in cui viene spiegato come risolvere le strutture iperstatiche utilizzando il teorema dei lavori virtuali li trovate nella pagina del Corso (pratico) di Meccanica Delle Strutture (dalla lezione 9 in poi).
Spostamenti e Deformazioni – Esercizio – 1.3

Guarda il video
(Pubblicazione 31.01.2024)
Nel video viene risolto un esercizio in cui, assegnato un campo di trasporto agente su una lamina, è richiesto di:
– determinare il campo di spostamento
– determinare il gradiente di trasporto verificandone l’invertibilità (impenetrabilità della materia)
– determinare il tensore della deformazione
– disegnare la lamina deformata
– determinare il tensore della tensione
Spostamenti e Deformazioni – Esercizio – 1.4

Guarda il video
(Pubblicazione 02.02.2024)
Assegnato il campo di spostamento u(x) determinare:
– il vettore traslazione e il vettore della rotazione rigida infinitesima;
– il tensore della deformazione infinitesima ;
– lo scorrimento angolare tra due fibre di direzione assegnata;
– la configurazione deformata di un quadrato di lato unitario;
Analisi della Tensione – 2.1
Guarda il video
(Pubblicazione 24.10.2023)
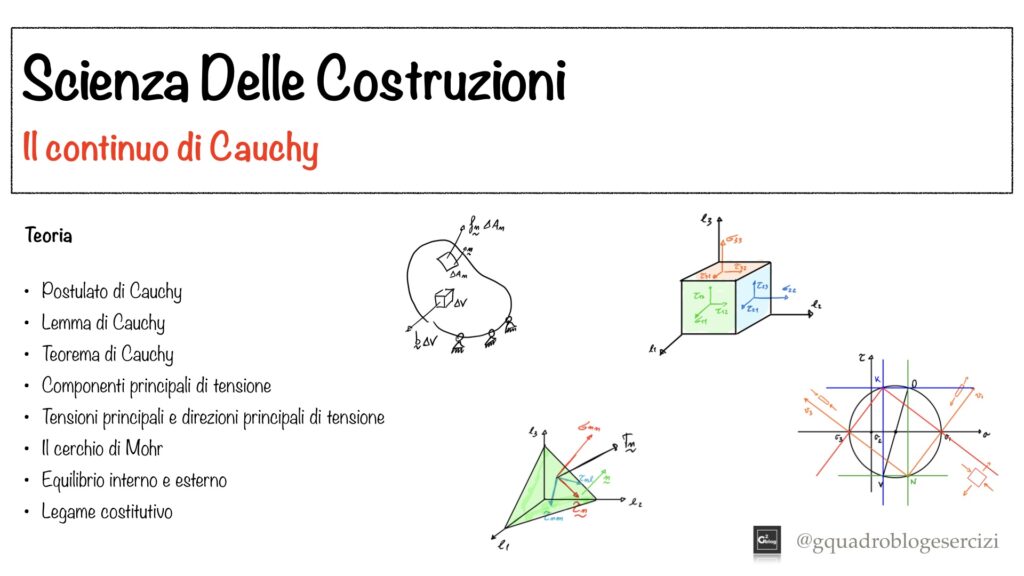
Nel video vengono spiegati i concetti fondamentali per la risoluzione di esercizi sul continuo di Cauchy (analisi della tensione). In particolare, vengono trattati in seguenti argomenti:
- Postulato, Lemma e Teorema di Cauchy
- Componenti principali di tensione
- Tensioni principali e direzioni principali di tensione
- Cerchio di Mohr
- Equilibrio interno ed esterno
- Legame costitutivo
Analisi della Tensione – 2.3

Guarda il video
(Pubblicazione 30.10.2023)
Nel video vengono risolti due esercizi relativi all’analisi della tensione.
Nel primo, assegnato un pannello quadrato su cui agiscono forze di contatto, viene richiesto di determinare il tensore della tensione, le tensioni principali e le direzioni principali di tensione, il tensore della deformazione.
Nel secondo viene assegnato un cubo su cui agiscono delle forze di contatto e viene richiesto di determinare lo stato di tensione (accertandosi che sia piano), il tensore della tensione, le tensioni principali e le direzioni principali di tensione, il tensore della deformazione.
Tensioni principali e direzioni principali di tensione vengono determinate con il cerchio di Mohr.
Saint Venant – Spiegazione fenomenologica e introduzione del problema di Forza Normale Eccentrica – 3.1

Guarda il video
(Pubblicazione 03.01.2024)
Nel video viene spiegato in modo pratico e fenomenologico il problema di Saint Venant: dalle azioni interne di una trave si passa alle tensioni agenti sui punti della sezione e quindi alle 4 casistiche principali del problema.
Viene poi analizzata e spiegata la casistica relativa a una Forza Normale Eccentrica agente in un punto di una sezione di una trave.
Viene dedotta la formula di Navier per la determinazione delle tensioni assiali generate dalla forza normale e vengono introdotti l’asse neutro, l’asse di sollecitazione e l’asse di flessione.
Saint Venant – Forza Normale Eccentrica – 3.2
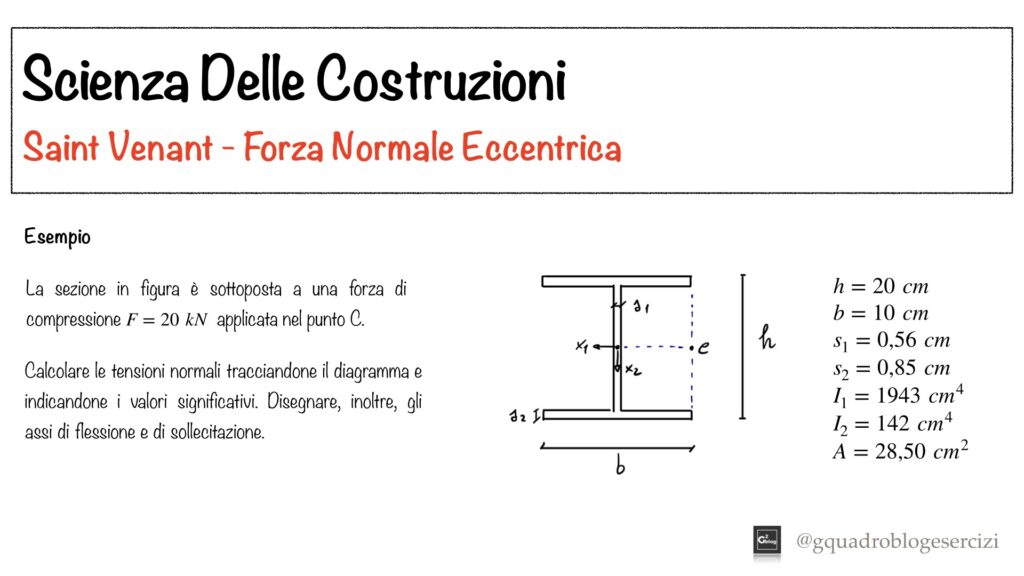
Nel video vengono determinate le tensioni assiali su una sezione a doppia T su cui agisce una forza normale eccentrica.
Le tensioni vengono determinate utilizzando la formula di Navier.
Oltre all’asse neutro vengono graficati gli assi di flessione e sollecitazione.
Saint Venant – Flessione retta e deviata – 4.1

Nel video vengono spiegati fenomenologicamente i concetti di flessione retta e deviata.
Viene poi fornita una spiegazione della curvatura flessionale.
Dopo l’introduzione teorico-pratica, viene risolto un esercizio in cui agisce una flessione deviata su una sezione quadrata cava.
Vengono determinati il diagramma delle tensioni assiali, l’espressione analitica delle tensioni assiali e i valori massimi e minimi da esse assunti.
Infine, vengono calcolate le componenti del vettore curvatura.
Saint Venant – Il problema di Taglio – 5.1

Guarda il video
(Pubblicazione 06.11.2023)
Nel video viene introdotto il problema di Taglio relativo al solido di Saint Venant.
In particolare, utilizzando un esempio viene spiegato come determinare le tensioni tangenziali prodotte su una sezione a causa dell’azione di una forza di taglio.
Dopo aver parlato del centro di taglio, viene introdotta la formula di Jourawsky e viene spiegato come calcolare i momenti di inerzia statici parametrizzati al fine di determinare l’andamento delle tensioni tangenziali sulla sezione.
Vengono, infine, disegnati i grafici della tensione tangenziale e del loro flusso nonché determinati i valori massimi che assume la tensione.
Saint Venant – Il problema di Taglio – 5.2
Guarda il video
(Pubblicazione 09.11.2023)
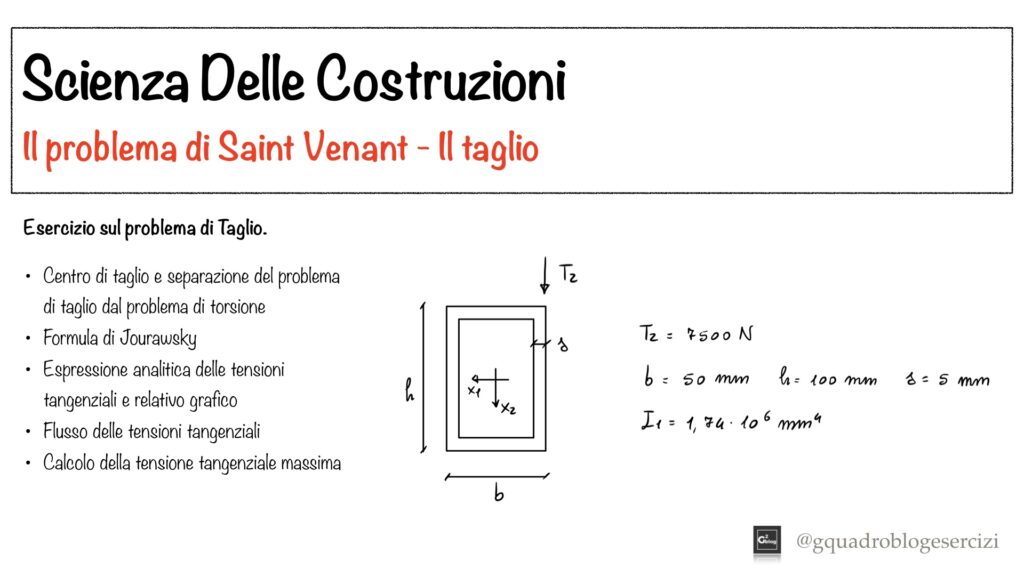
Nel video viene risolto un problema di taglio relativo al solido di Saint Venant.
In particolar modo, viene analizzata una sezione rettangolare cava su cui agisce una forza di taglio non passante per il centro di taglio.
Dopo aver separato il problema di taglio dal problema di torsione, vengono determinate le tensioni tangenziali dovute al taglio utilizzando la formula di Jourawsky.
Vengono, disegnati i grafici della tensione tangenziale e del loro flusso nonché determinati i valori massimi che assume la tensione.
Saint Venant – Il problema di Taglio – 5.3
Guarda il video
(Pubblicazione 27.12.2023)
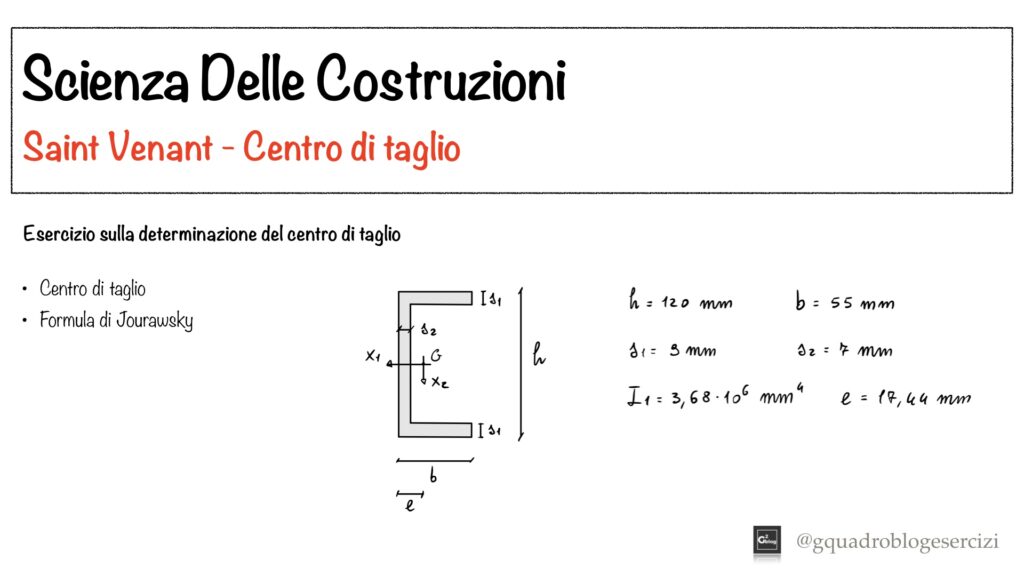
Nel video viene spiegato come determinare il centro di taglio di una sezione e viene svolto un esercizio in cui ne è richiesto il calcolo per una sezione a C.
Saint Venant – Il Taglio su una sezione circolare cava – 5.4

Guarda il video
(Pubblicazione 18.01.2024)
Nel video viene risolto un problema di taglio relativo al solido di Saint Venant.
In particolar modo, viene analizzata una sezione circolare cava (corona circolare) di piccolo spessore su cui agisce una forza di taglio passante per il centro di taglio.
Vengono determinate le tensioni tangenziali dovute al taglio utilizzando la formula di Jourawsky e vengono disegnati i grafici della tensione tangenziale determinando il valore massimo di quest’ultima.
Dopo l’esercizio viene ripassato il concetto di momento di inerzia polare (traccia del tensore di inerzia) e lo si calcola per un cerchio.
Saint Venant – Il problema di Torsione – 6.1
Guarda il video
(Pubblicazione 03.12.2023)
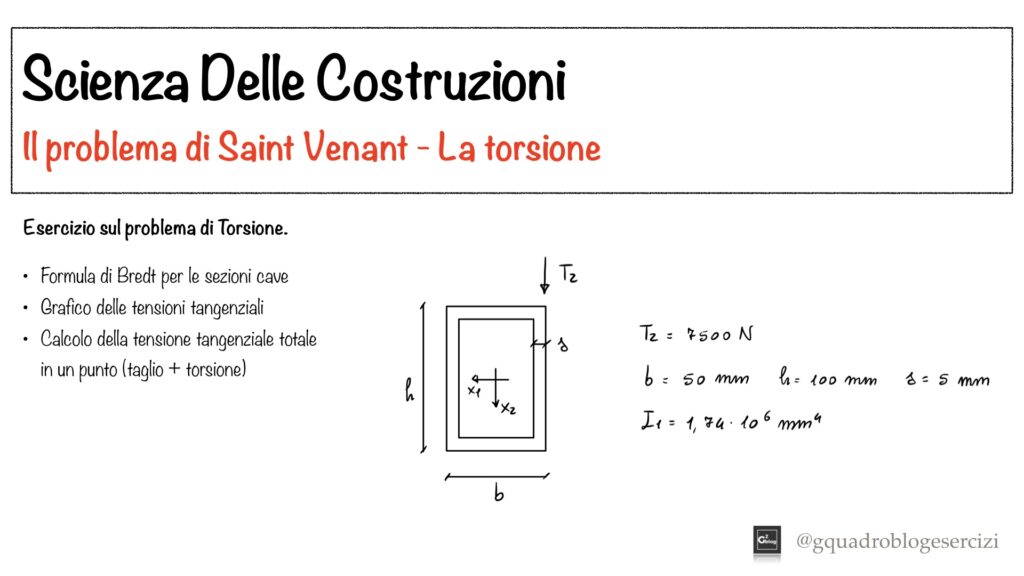
Nel video viene risolto un problema di torsione relativo al solido di Saint Venant.
Partendo dalla sezione risolta nel video precedente, in cui si separa il problema di taglio dal problema di torsione, vengono determinate le tensioni tangenziali dovute al momento torcente.
Poiché la sezione è cava, le tensioni vengono determinate utilizzando la formula di Bredt.
Vengono infine disegnati i grafici e viene calcolata la tensione tangenziale totale in un punto (somma della tensione tangenziale dovuta al taglio, calcolata nel video precedente, e della tensione tangenziale dovuta alla torsione).
Saint Venant – Il problema di Torsione 6.2

Guarda il video
(Pubblicazione 09/12/2023)
Nel video viene risolto un problema di torsione relativo al solido di Saint Venant.
Data una sezione circolare cava, vengono determinate le tensioni tangenziali utilizzando prima la formula esatta (con il calcolo del momento di inerzia polare) e poi la formula approssimata di Bredt.
Vengono infine disegnati i grafici e confrontati i valori ottenuti.
Saint Venant – Verifica di una sezione 7.1
Guarda il video
(Pubblicazione 14/12/2023)
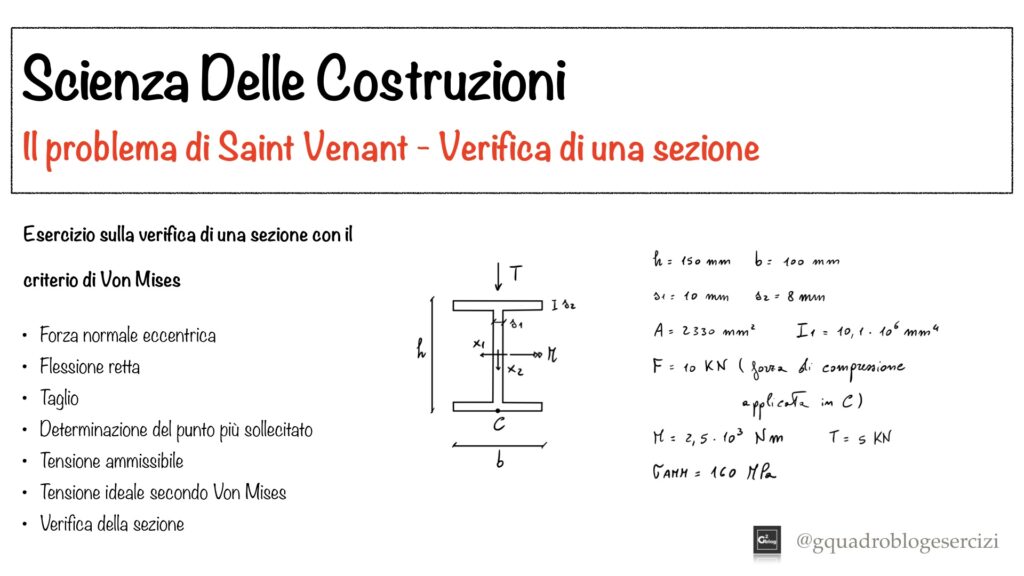
Nel video vengono determinate le tensioni assiali e tangenziali su una sezione.
Sulla sezione agiscono una forza normale eccentrica, un momento flettente e una forza di taglio.
Viene poi determinato il punto più sollecitato della sezione e effettuata la sua verifica con il criterio di Von Mises.
Geometria delle Aree 8.1
Guarda il video
(Pubblicazione 24/12/2023)
Nel video vengono riepilogate alcune formule inerenti alla geometria delle aree:
– baricentro
– momenti di inerzia statici
– momenti di inerzia del secondo ordine
– teorema di Huygens
– momenti di inerzia principali e sistema di riferimento principale di inerzia.
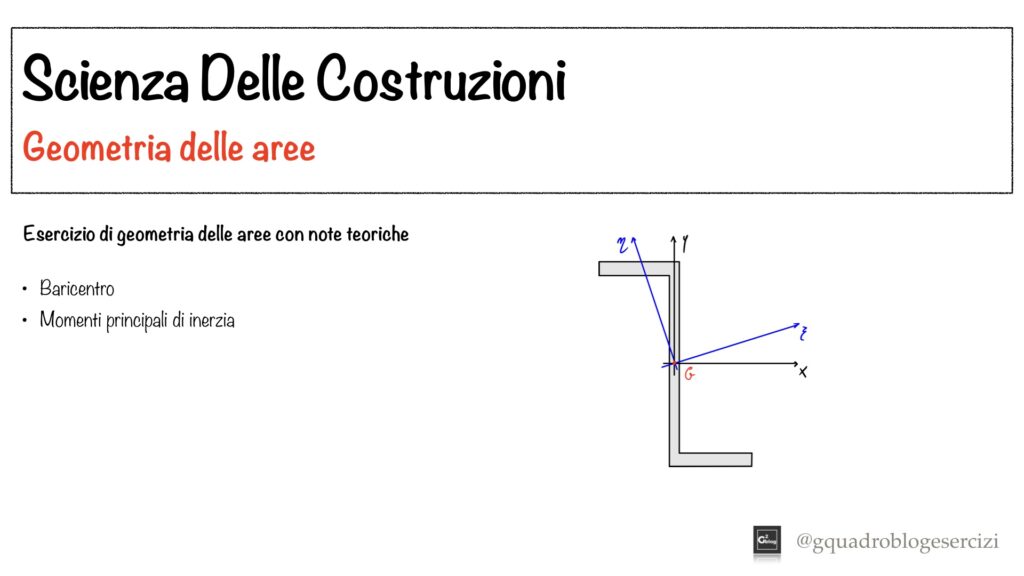
Viene poi risolto un esercizio in cui si determinano i momenti principali di inerzia per una sezione a Z.
SdC- Esercizi di riepilogo – 9.1

Guarda il video
(Pubblicazione 24.01.2024)
Nel video, dopo aver calcolato i momenti di inerzia di una sezione a T rovesciata, vengono determinate le tensioni assiali e tangenziali dovute a una forza normale centrata e a una forza di taglio verticale passante per il centro di taglio.
Vengono poi determinate le tensioni principali nel punto maggiormente sollecitato mediante il cerchio di Mohr.
Utilizzando il legame costitutivo viene, infine, determinato il tensore della deformazione.