Dal punto di vista geometrico un integrale doppio della forma
\iint _D f(x,y) dxdy
può essere interpretato come il volume del solido ottenuto estendendo la regione di piano D fino al grafico della funzione ![]() :
:
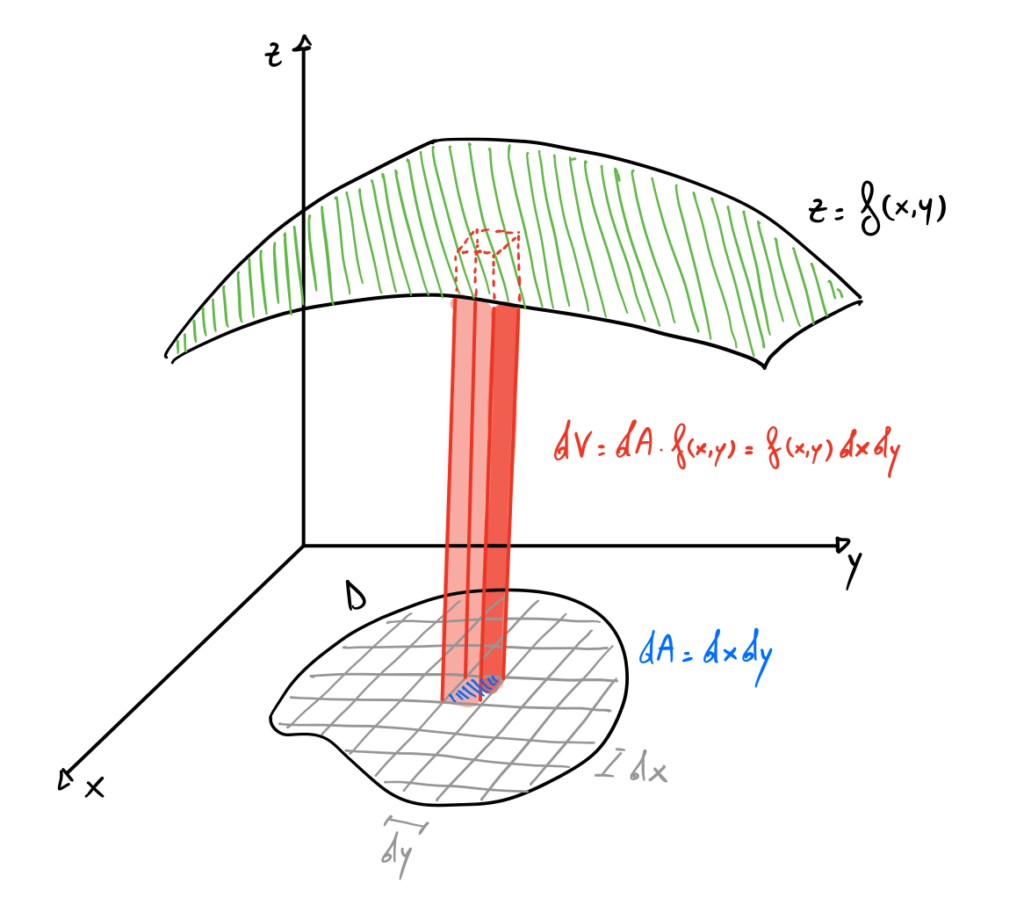
Il termine ![]() rappresenta, infatti, il volume del parallelepipedo infinitesimo avente area di base
rappresenta, infatti, il volume del parallelepipedo infinitesimo avente area di base ![]() e altezza data da (
e altezza data da (![]() ). Con l’integrale doppio si sommano poi i volumi degli infiniti parallelepipedi infinitesimi.
). Con l’integrale doppio si sommano poi i volumi degli infiniti parallelepipedi infinitesimi.
Per calcolare un integrale doppio è, quindi, necessario che l’insieme di integrazione D sia misurabile. Ci concentreremo in particolare su tre eventualità:
- D è rettangolare
- D è un dominio normale
- D è un dominio circolare
Vediamo le formule risolutive dell’integrale in queste tre casistiche.
1) D è di forma rettangolare
D=\{ (x,y)\in \mathbb R^2 : a\leq x \leq b, c \leq y \leq d \}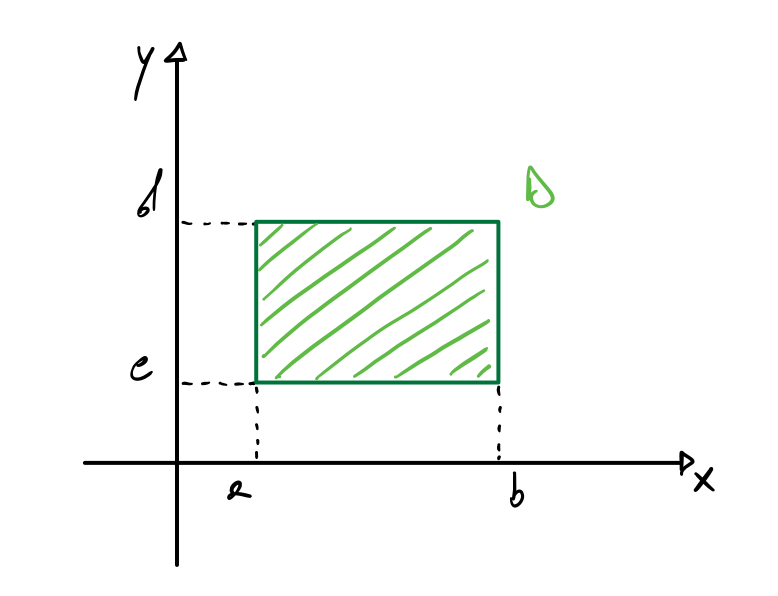
In questi casi la soluzione dell’integrale doppio è allora data da:
\iint_D f(x,y)dxdy = \int_c^d \bigg(\int_a^b f(x,y)dx \bigg)dy = \int_a^b \bigg(\int_c^d f(x,y)dy \bigg)dx
Esempio 1
Calcolare il seguente integrale doppio:
\iint_D(x^2+y)dxdy \ \ \ \ \ \text{con} \ \ D =\{(x,y)\in \mathbb{R^2} : x\in[1,2], y\in [0,1] \}Svolgimento
Analizzando il dominio si vede che sia la ![]() che la
che la ![]() sono compresi tra due numeri: il dominio è di tipo rettangolare.
sono compresi tra due numeri: il dominio è di tipo rettangolare.
Risolviamo l’integrale integrando prima rispetto alla variabile ![]() e poi rispetto alla variabile
e poi rispetto alla variabile ![]() (avremmo potuto anche fare il contrario).
(avremmo potuto anche fare il contrario).
\begin{aligned}
&\int_1^2 \Bigg(\int_0^1(x^2+y)dy\Bigg)dx =\int_1^2\bigg( x^2y+\frac{y^2}{2} \bigg)\bigg|_0^1 dx =
\int_1^2\bigg( x^2+\frac{1}{2} \bigg) dx =\bigg( \frac{x^3}{3}+\frac{1}{2}x\bigg)\bigg|_1^2= \\
&=\frac{8}{3} +\frac{2}{2}-\frac{1}{3}-\frac{1}{2}=\frac{17}{6}
\end{aligned}2) D è un dominio normale
2.1) Dominio normale rispetto all’asse x
D=\{ (x,y)\in \mathbb R^2 : a\leq x \leq b, g(x) \leq y \leq h(x) \}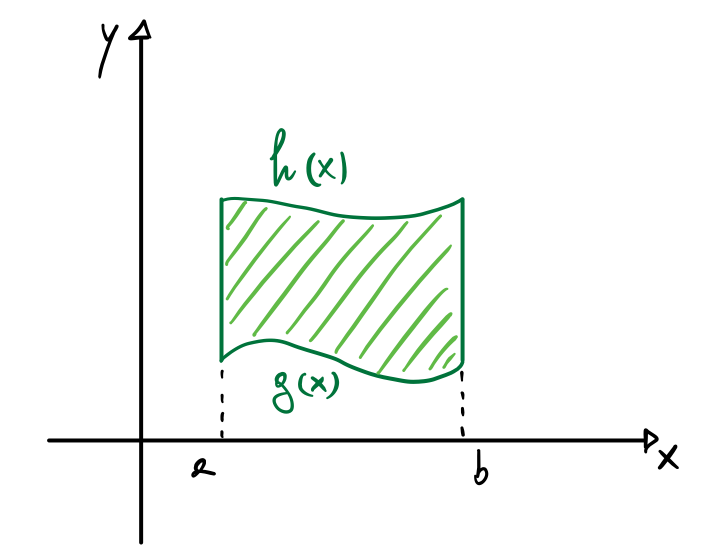
In questi casi la soluzione dell’integrale è data da:
\iint_D f(x,y)dxdy = \int_a^b \bigg(\int_{g(x)}^{h(x)} f(x,y)dy \bigg)dx2.2) Dominio normale rispetto all’asse y
D=\{ (x,y)\in \mathbb R^2 : c\leq y \leq d, g(y) \leq x \leq h(y) \}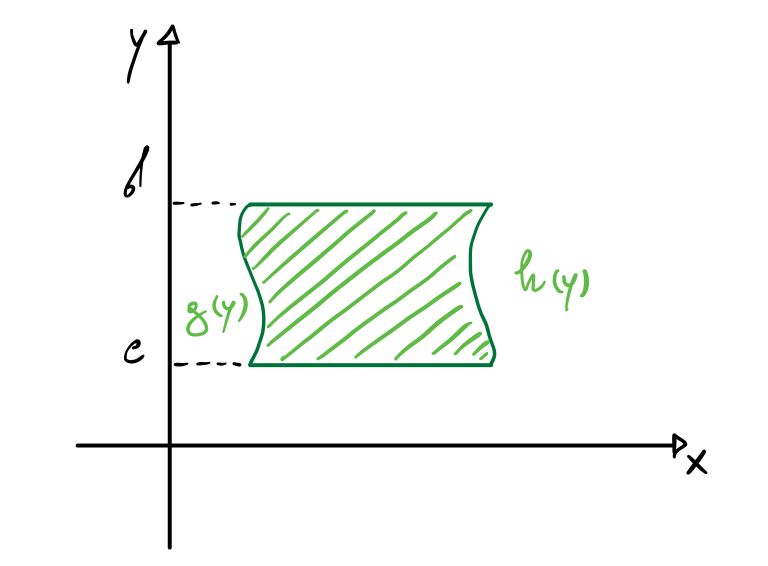
In questi casi la soluzione dell’integrale è data da:
\iint_D f(x,y)dxdy = \int_c^d \bigg(\int_{g(y)}^{h(y)} f(x,y)dx \bigg)dyEsempio 2
Calcolare il seguente integrale doppio:
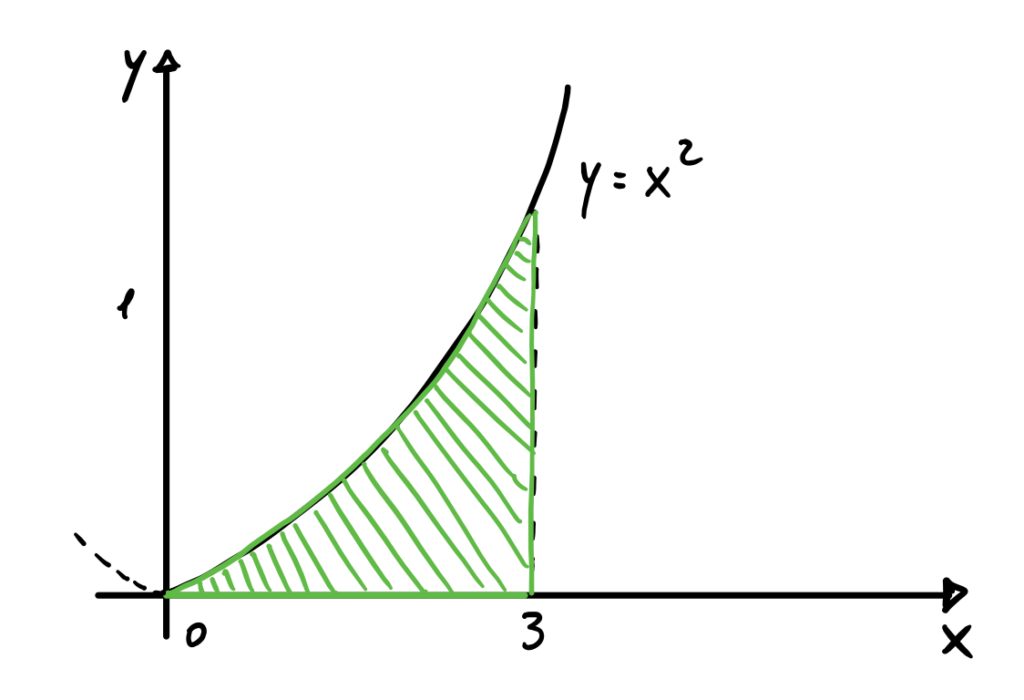
\iint_D(x+1)ydxdy \ \ \ \ \ \text{con} \ \ D =\{(x,y)\in \mathbb{R^2} : x\in[0,3], 0 \leq y \leq x^2 \}Svolgimento
Analizzando il dominio si vede che sia la ![]() varia tra due numeri e la
varia tra due numeri e la ![]() tra due funzioni di
tra due funzioni di ![]() : il dominio è normale rispetto a
: il dominio è normale rispetto a ![]() .
.
Risolviamo l’integrale integrando prima rispetto alla variabile ![]() (cioè quella che varia tra le due funzioni) e poi rispetto alla variabile
(cioè quella che varia tra le due funzioni) e poi rispetto alla variabile ![]() .
.
\begin{aligned}
&\int_0^3 \Bigg(\int_0^{x^2}(x+1)ydy\Bigg)dx =
\int_0^3 (x+1) \frac{y^2}{2}\bigg|_0^{x^2} dx =
\int_0^3 (x+1)\frac{x^4}{2}dx = \\
& =\frac{1}{2} \int_0^3\big(x^5+x^4 \big)dx =
\frac{1}{2}\bigg( \frac{x^6}{6}+\frac{x^5}{5}\bigg)\bigg|_0^3=
\frac{1}{2}\bigg( \frac{3^6}{3\cdot 2}+\frac{3^5}{5}\bigg)=
\frac{1}{2}\bigg( \frac{3^5}{2}+\frac{3^5}{5}\bigg)= \\
&=\frac{1687}{20}
\end{aligned}3) D è un dominio circolare
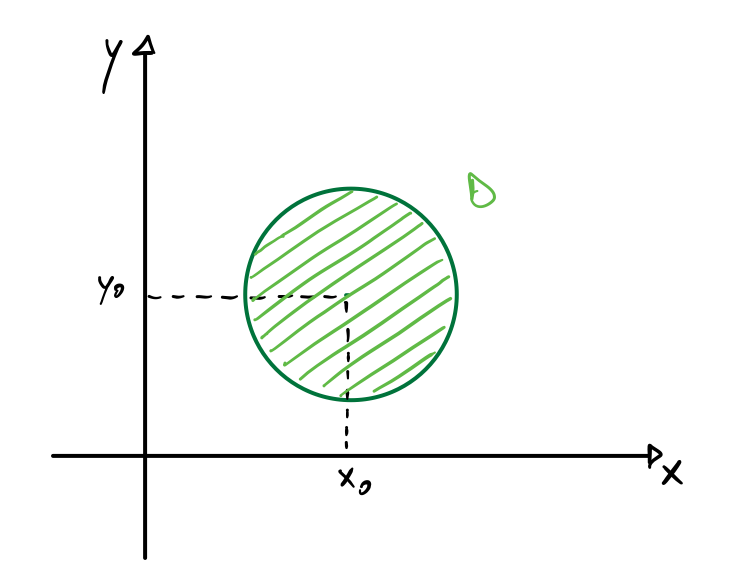
In questi casi può essere vantaggioso risolvere l’integrale utilizzando le coordinate polari di centro ![]() :
:
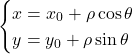
Ovviamente si ha che:
![]() .
.
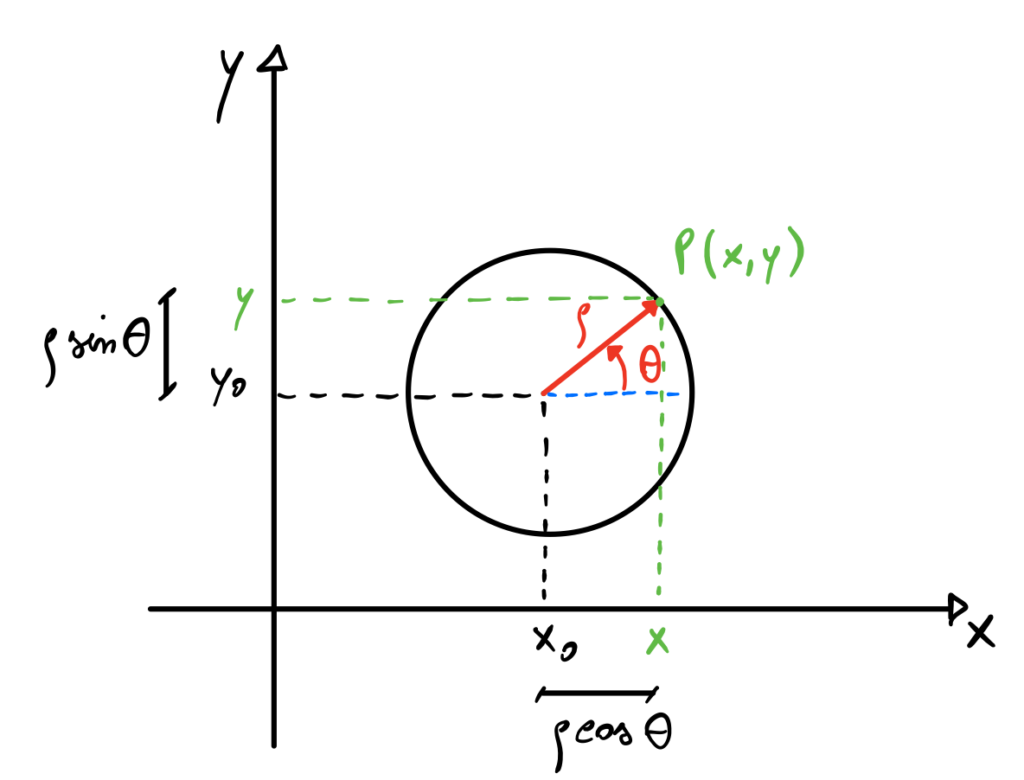
Quando si passa dalle coordinate cartesiane ![]() alle coordinate polari
alle coordinate polari ![]() bisogna tenere conto del cambio di misura dell’area infinitesima
bisogna tenere conto del cambio di misura dell’area infinitesima ![]() :
:
dxdy=\rho d\rho d\theta
con ![]() (Modulo del determinante della matrice Jacobiana).
(Modulo del determinante della matrice Jacobiana).
L’integrale riscritto in coordinate polari diventa:
\iint_{D_{\rho,\theta}}f(x_0 + \rho\cos \theta, y_0 + \rho\sin \theta)\rho d\rho d\thetaEsempio 3
Calcolare il seguente integrale doppio:
\iint_Dxdxdy \ \ \ \ \ \text{con} \ \ D =\{(x,y)\in \mathbb{R^2} : x\geq0, x^2+y^2\leq 1 \}Svolgimento
Analizzando il dominio si vede che si tratta del semicerchio centrato nell’origine e di raggio 1: un dominio circolare
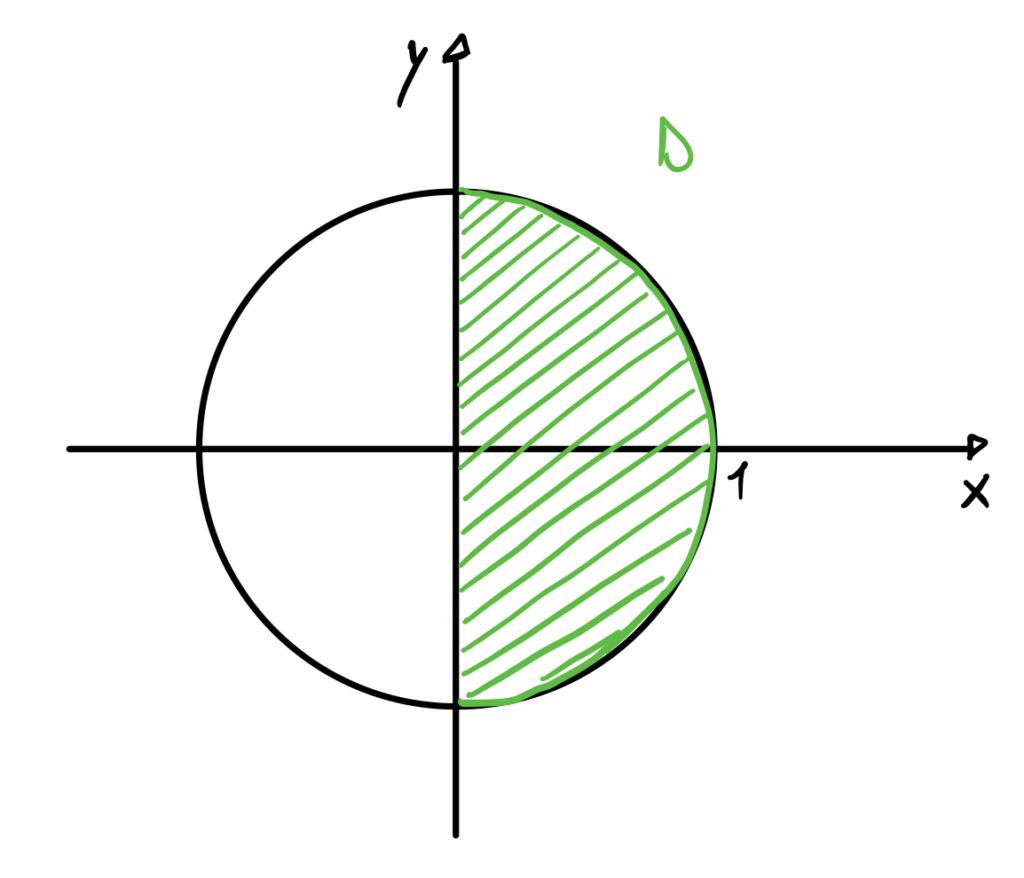
Risolviamo l’integrale utilizzando le coordinate polari di centro l’origine:
\begin{cases}
x=\rho\cos (\theta) \\
y = \rho \sin (\theta)
\end{cases} \ \ \ \text{con} \ \ \rho \in [0,1], \ \theta \in \Big[-\frac{\pi}{2},\frac{\pi}{2}\Big], \ \ |\det \mathbf J|=\rho \ \ \text{e} \ \ x^2+y^2=\rho^2Sostituendo nell’integrale otteniamo:
\begin{aligned}
&\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \Bigg(\int_0^1 \rho\cos \theta\cdot \rho d\rho\Bigg)d\theta =\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \Bigg(\int_0^1 \rho^2\cos \theta d\rho\Bigg)d\theta =
\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \cos \theta d\theta \int_0^1 \rho^2 d\rho = \\ \\
& = \sin \theta\bigg|_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\cdot \frac{\rho^3}{3}\bigg|_0^1 =
(1-(-1))\cdot \frac{1}{3}=\frac{2}{3}
\end{aligned}Osservazione 1
Dall’interpretazione geometrica dell’integrale doppio segue che
\iint_D 1 \ dxdy
rappresenta l’area della regione ![]() , dal momento che
, dal momento che
Volume = Area \ base \times Altezza = Area \ D \times 1 = Area \ D
Osservazione 2
Se ![]() è dispari rispetto a
è dispari rispetto a ![]() e il dominio è simmetrico rispetto a
e il dominio è simmetrico rispetto a ![]() , si ha che
, si ha che
\iint_D f(x,y) \ dxdy =0.
Lo stesso accade se ![]() è dispari rispetto a
è dispari rispetto a ![]() e il dominio è simmetrico rispetto a
e il dominio è simmetrico rispetto a ![]() .
.
Osservazione 2.1
![]() è dispari rispetto a
è dispari rispetto a ![]() se
se ![]() ;
;
![]() è dispari rispetto a
è dispari rispetto a ![]() se
se ![]() ;
;
L’integrale doppio è nullo perchè il “Volume negativo” è uguale al “Volume positivo” cosicché la loro somma è zero.