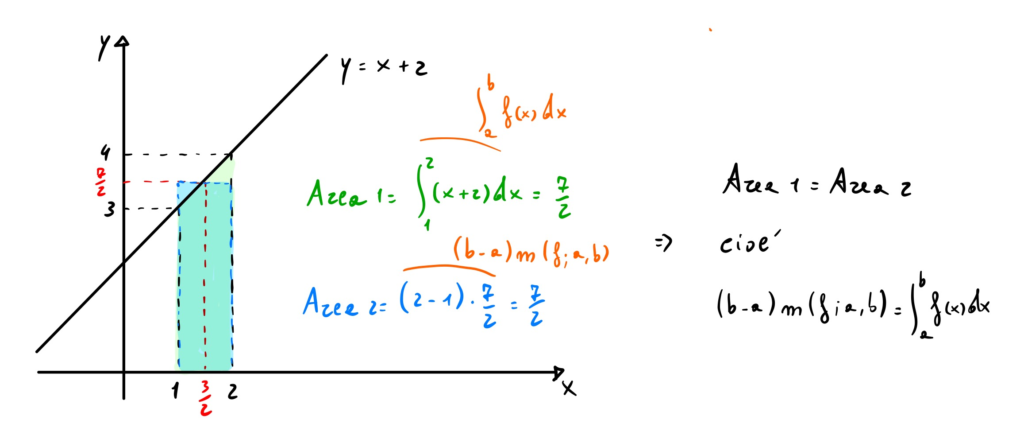Enunciato
Sia ![]() una funzione integrabile su un intervallo
una funzione integrabile su un intervallo ![]() . La media integrale di
. La media integrale di ![]() su
su ![]() definita come
definita come ![]() soddisfa le seguenti disuguaglianze:
soddisfa le seguenti disuguaglianze:
\inf_{x\in \left[ a,b\right] }f(x) \leq m(f;a,b) \leq \sup_{x\in [a,b]} f(x) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (1)Inoltre, se ![]() è continua su
è continua su ![]() , esiste almeno un punto
, esiste almeno un punto ![]() tale che
tale che ![]() .
.
Dimostrazione
Poniamo ![]() e
e ![]() .
.
Per ogni ![]() si ha che
si ha che ![]() . Integrando tutti i membri tra
. Integrando tutti i membri tra ![]() e
e ![]() otteniamo:
otteniamo:
\int_a^b s dx\leq \int_a^b f(x)dx \leq \int_a^b Sdx \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2)
Osservando che le quantità ![]() e
e ![]() sono costanti, il primo e l’ultimo integrale diventano:
sono costanti, il primo e l’ultimo integrale diventano:
![]()
che sostituite nella (2) forniscono:
![]()
da cui, dividendo per ![]() , si ha
, si ha
![]()
che è proprio quanto volevamo dimostrare.
Dimostriamo ora la seconda parte del teorema.
Se ![]() è continua su
è continua su ![]() allora
allora ![]() assume su
assume su ![]() i valori minimo e massimo assoluti. Infatti, il teorema di Weierstrass ci assicura che se
i valori minimo e massimo assoluti. Infatti, il teorema di Weierstrass ci assicura che se ![]() è continua su un intervallo chiuso e limitato
è continua su un intervallo chiuso e limitato ![]() ,
, ![]() assume su tale intervallo i valori massimo e minimo assoluti (rispettivamente
assume su tale intervallo i valori massimo e minimo assoluti (rispettivamente ![]() e
e ![]() ) e, inoltre, l’immagine di
) e, inoltre, l’immagine di ![]() su
su ![]() corrisponde all’intervallo
corrisponde all’intervallo ![]() (ossia, per
(ossia, per ![]() assume tutti i valori dell’intervallo
assume tutti i valori dell’intervallo ![]() ).
).
Nel caso di funzione continua su ![]() si ha che l’estremo inferiore di
si ha che l’estremo inferiore di ![]() corrisponde al minimo assoluto
corrisponde al minimo assoluto ![]() e l’estremo superiore di
e l’estremo superiore di ![]() corrisponde al massimo assoluto
corrisponde al massimo assoluto ![]() . Di conseguenza la (1) diventa
. Di conseguenza la (1) diventa
![]()
e ciò ci assicura che il valore medio integrale appartenga all’intervallo ![]() . Dato che, per il teorema di Weierstrass, tale intervallo è l’immagine di
. Dato che, per il teorema di Weierstrass, tale intervallo è l’immagine di ![]() su
su ![]() deve necessariamente esistere un punto
deve necessariamente esistere un punto ![]() tale che
tale che ![]() .
.
Con ciò abbiamo dimostrato anche la seconda parte del teorema.
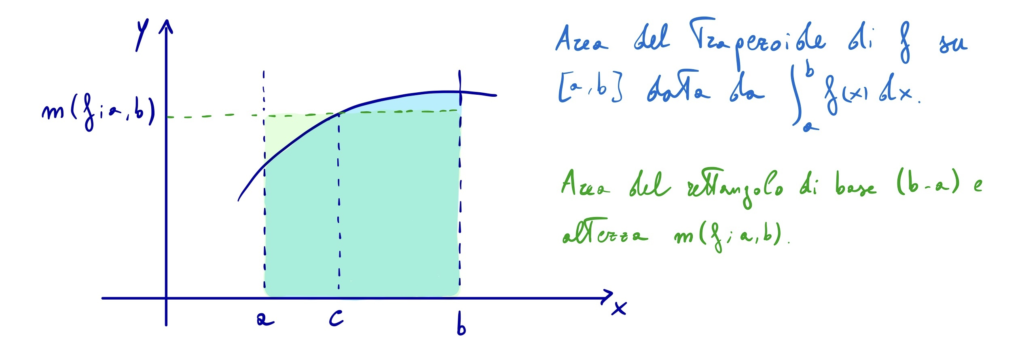
Significato geometrico del teorema
Nel caso di funzione positiva e continua su ![]() , si può facilmente vedere che il teorema della media integrale implica l’equivalenza tra l’area del trapezoide di
, si può facilmente vedere che il teorema della media integrale implica l’equivalenza tra l’area del trapezoide di ![]() su
su ![]() e l’area del rettangolo avente base
e l’area del rettangolo avente base ![]() e altezza
e altezza ![]() :
:
Esempio
Verificare la validità del teorema della media integrale per la funzione ![]() sull’intervallo
sull’intervallo ![]() .
.
Svolgimento
Calcoliamo prima di tutto il valore medio integrale della funzione:
![]()
A questo punto dobbiamo trovare il valore ![]() tale che
tale che ![]() e verificare che
e verificare che ![]() .
.
![]()
Poiché ![]() il teorema risulta verificato.
il teorema risulta verificato.
Mostriamo anche l’aspetto geometrico.