Nell’articolo che segue consideriamo campi vettoriali della forma ![]() : sono delle funzioni che prendendo in ingresso due input
: sono delle funzioni che prendendo in ingresso due input ![]() e
e ![]() restituiscono in uscita due output
restituiscono in uscita due output ![]() e
e ![]() .
.
Il campo vettoriale verrà allora scritto come:
![]()
Quando studiamo un campo vettoriale siamo in particolar modo interessati a 3 sue proprietà: il dominio, la rotazionalità e la conservatività.
Vediamole nel dettaglio.
1) Il dominio
Il dominio di un campo vettoriale è dato dall’intersezione dei domini delle due funzioni che costituiscono il campo vettoriale:
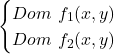
1.2) Studio della natura del dominio
Nello studio dei campi vettoriali è importante classificare l’insieme in cui si sta effettuando tale studio. In particolare è necessario capire se l’insieme è semplicemente connesso o meno.
Un insieme viene definito semplicemente connesso se ogni curva chiusa in esso contenuta è omotopa a un punto, ossia se ogni curva chiusa contenuta nell’insieme piò essere deformata con continuità fino a diventare un punto.

In ![]() possiamo asserire che un insieme è semplicemente connesso se e solo se non ha buchi.
possiamo asserire che un insieme è semplicemente connesso se e solo se non ha buchi.
Osservazione 1
Un insieme semplicemente connesso privato di una retta continua ad essere semplicemente connesso in quanto può essere considerato unione di due insiemi semplicemente connessi.
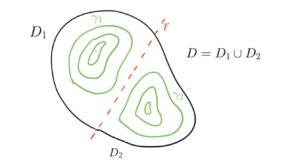
3) Studio della rotazionalità
Un campo vettoriale viene definito irrotazionale se
![]()
4) Studio della conservatività
Un campo vettoriale ![]() viene definito conservativo se esiste una funzione
viene definito conservativo se esiste una funzione ![]() tale che:
tale che:
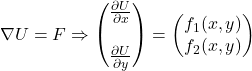
In tal caso la funzione ![]() si dice potenziale del campo vettoriale
si dice potenziale del campo vettoriale ![]() .
.
4.1) Calcolo del potenziale del campo vettoriale ![]()
Per calcolare il potenziale del campo vettoriale ![]() utilizziamo la definizione data al punto precedente:
utilizziamo la definizione data al punto precedente:
dobbiamo calcolare una funzione ![]() tale che la derivata di
tale che la derivata di ![]() rispetto a
rispetto a ![]() sia pari a
sia pari a ![]() e la derivata di
e la derivata di ![]() rispetto a
rispetto a ![]() sia paria a
sia paria a ![]() .
.
Per far ciò o integriamo ![]() rispetto a
rispetto a ![]() oppure
oppure ![]() rispetto a
rispetto a ![]() . La costante di integrazione sarà funzione della variabile rispetto alla quale non abbiamo svolto l’integrale.
. La costante di integrazione sarà funzione della variabile rispetto alla quale non abbiamo svolto l’integrale.
Ad esempio, integrando ![]() rispetto a
rispetto a ![]() otteniamo:
otteniamo:
![]()
A questo punto dobbiamo porre la derivata di ![]() rispetto a
rispetto a ![]() uguale a
uguale a ![]() :
:
![]()
A questo punto ricavando ![]() (integrando la relazione precedente rispetto a
(integrando la relazione precedente rispetto a ![]() e sostituendo l’espressione di
e sostituendo l’espressione di ![]() nell’espressione del potenziale
nell’espressione del potenziale ![]() otteniamo la forma finale del potenziale di
otteniamo la forma finale del potenziale di ![]() .
.
Osservazione 2
Se ![]() è irrotazionale in un insieme semplicemente connesso allora
è irrotazionale in un insieme semplicemente connesso allora ![]() è conservativo.
è conservativo.
Osservazione 3
Se ![]() è irrotazionale su un insieme che non è semplicemente connesso possiamo verificarne la conservatività calcolandone l’integrale lungo una curva chiusa che circonda il “buco”: se l’integrale è zero allora
è irrotazionale su un insieme che non è semplicemente connesso possiamo verificarne la conservatività calcolandone l’integrale lungo una curva chiusa che circonda il “buco”: se l’integrale è zero allora ![]() è conservativo.
è conservativo.
Vediamo ora un esempio di studio di un campo vettoriale.
Esempio 1
Dati il dominio ![]() e il campo vettoriale
e il campo vettoriale ![]() determinare se esso sia conservativo su
determinare se esso sia conservativo su ![]() .
.
Svolgimento
1) Dominio
Per prima cosa calcoliamo il dominio di ![]() :
:
![]() .
.
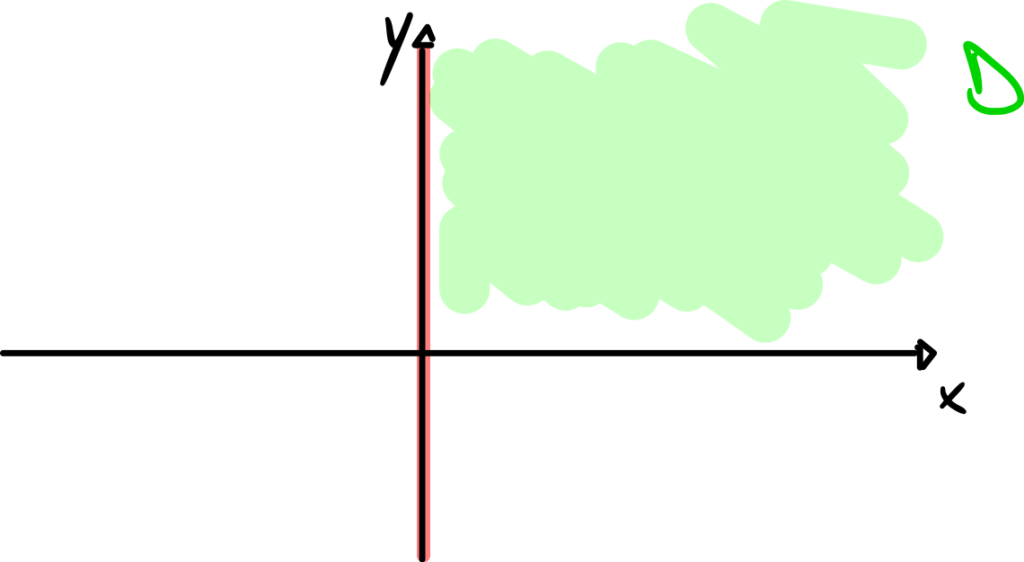
Si vede che il campo vettoriale è ben definito nell’insieme ![]() .
.
Poiché l’insieme ![]() non ha buchi possiamo concludere che esso è semplicemente connesso.
non ha buchi possiamo concludere che esso è semplicemente connesso.
2) Irrotazionalità
Studiamo la rotazionalità del campo vettoriale.
![]()
![]()
Poiché ![]() il campo vettoriale è irrotazionale.
il campo vettoriale è irrotazionale.
3) Conservatività
Dato che il campo vettoriale ![]() è irrotazionale sull’insieme semplicemente connesso
è irrotazionale sull’insieme semplicemente connesso ![]() si ha che
si ha che ![]() è conservativo su
è conservativo su ![]() esiste il potenziale
esiste il potenziale ![]() di
di ![]() .
.
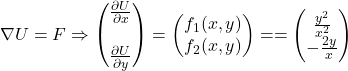
Integriamo ![]() rispetto a y:
rispetto a y:
![]()
Deriviamo ![]() rispetto a x e poniamo il risultato pari a
rispetto a x e poniamo il risultato pari a ![]() :
:
![]()
![]()
![]()
Sostituendo ![]() nell’espressione di
nell’espressione di ![]() determinata precedentemente otteniamo il potenziale di
determinata precedentemente otteniamo il potenziale di ![]() :
:
![]()
