Nel 1787 il fisico e musicista Ernst Florence Friedrich Chladni fece un’interessante scoperta: eccitando con l’arco del suo violino una piastra metallica, fissata solo al centro, riusciva a ottenere suoni di intonazione differente a seconda del punto della piastra che sollecitava. Successivamente, si accorse che se sulla piastra si depositava della polvere, o vi si disponeva della sabbia, per ogni intonazione apparivano pattern differenti e magnifici. Nel suo libro sull’acustica, Chladni descrisse diversi esperimenti con le piastre vibranti determinando anche le frequenze corrispondenti ai vari pattern che otteneva.  Le figure di Chladni, così come vengono chiamate oggi, attirarono l’attenzione di molti scienziati, e non solo. Nel 1809 il fisico fu invitato dall’Accademia Francese delle Scienze a effettuare i suoi esperimenti in pubblico. A tale spettacolo presenziò anche l’imperatore Napoleone, che rimase parecchio impressionato dalla dimostrazione dello scienziato. Seguendo il suggerimento dell’imperatore, l’Accademia bandì un concorso richiedendo un saggio scientifico concernente la piastra vibrante, in cui i risultati sperimentali fossero giustificati da una teoria matematica. All’inizio non fu inviato alcun documento cosicchè la durata del bando venne prolungata. Alla fine, nell’ottobre del 1811, il giorno di chiusura del concorso, l’Accademia ricevette solo un articolo intitolato “Reserches sur la theorie des surfaces elastiques”, scritto dalla matematica Sophie Germain. Lagrange, che era uno dei giudici, notò un errore matematico nella teoria presentata e lo corresse. Non essendo completamente soddisfatti dal lavoro di Germain, i giudici decisero di riproporre l’argomento. Nell’ottobre del 1813, Sophie Germain inviò una rivisitazione del suo lavoro, che risultò ancora inadeguato. Al suo terzo tentativo, nel 1826, il lavoro della scienziata suscitò ancora critiche, dal momento che conteneva ragionamenti matematici e fisici poco chiari, ma si decise comunque di premiare il suo coraggio e la sua determinazione assegnandole il premio. Migliorie successive alla soluzione del problema furono apportate da Poisson, che non riuscì, tuttavia, a risolverlo totalmente. Alla finne, fu il famoso ingegnere e scienziato L. Navier che pervenne alla prima equazione differenziale corretta per le piastre soggette a carichi statici distribuiti. Navier applicò le ipotesi di Bernoulli, già utilizzate con successo nello studio della deflessione delle travi, aggiungendovi, però, le altre due dimensioni. Dopo aver determinato l’equazione differenziale, lo scienziato ne cercò la soluzione. Per alcune condizioni al contorno Navier introdusse un metodo che trasformava l’equazione differenziale in un’equazione algebrica. Il suo approccio era basato sull’utilizzo delle serie trigonometriche introdotte da Fourier nello stesso decennio. Purtroppo, fallì nel tentativo di risolvere i casi più complessi. Fu Gustav R. Kirchhoff che sviluppò la prima teoria completa della piastra infessa. Egli ottenne la medesima equazione di Navier riuscendo, però, a esprimere tutte le condizioni al contorno in funzione dello spostamento trasversale e delle sue derivate rispetto a x e a y. Uno dei suoi contributi più significativi fu l’introduzione del metodo degli spostamenti virtuali per la risoluzione di vari problemi riguardanti le piastre. Kirchhoff espose il suo lavoro in un lungo articolo del 1850. L’equazione a cui pervenne fu la seguente:
Le figure di Chladni, così come vengono chiamate oggi, attirarono l’attenzione di molti scienziati, e non solo. Nel 1809 il fisico fu invitato dall’Accademia Francese delle Scienze a effettuare i suoi esperimenti in pubblico. A tale spettacolo presenziò anche l’imperatore Napoleone, che rimase parecchio impressionato dalla dimostrazione dello scienziato. Seguendo il suggerimento dell’imperatore, l’Accademia bandì un concorso richiedendo un saggio scientifico concernente la piastra vibrante, in cui i risultati sperimentali fossero giustificati da una teoria matematica. All’inizio non fu inviato alcun documento cosicchè la durata del bando venne prolungata. Alla fine, nell’ottobre del 1811, il giorno di chiusura del concorso, l’Accademia ricevette solo un articolo intitolato “Reserches sur la theorie des surfaces elastiques”, scritto dalla matematica Sophie Germain. Lagrange, che era uno dei giudici, notò un errore matematico nella teoria presentata e lo corresse. Non essendo completamente soddisfatti dal lavoro di Germain, i giudici decisero di riproporre l’argomento. Nell’ottobre del 1813, Sophie Germain inviò una rivisitazione del suo lavoro, che risultò ancora inadeguato. Al suo terzo tentativo, nel 1826, il lavoro della scienziata suscitò ancora critiche, dal momento che conteneva ragionamenti matematici e fisici poco chiari, ma si decise comunque di premiare il suo coraggio e la sua determinazione assegnandole il premio. Migliorie successive alla soluzione del problema furono apportate da Poisson, che non riuscì, tuttavia, a risolverlo totalmente. Alla finne, fu il famoso ingegnere e scienziato L. Navier che pervenne alla prima equazione differenziale corretta per le piastre soggette a carichi statici distribuiti. Navier applicò le ipotesi di Bernoulli, già utilizzate con successo nello studio della deflessione delle travi, aggiungendovi, però, le altre due dimensioni. Dopo aver determinato l’equazione differenziale, lo scienziato ne cercò la soluzione. Per alcune condizioni al contorno Navier introdusse un metodo che trasformava l’equazione differenziale in un’equazione algebrica. Il suo approccio era basato sull’utilizzo delle serie trigonometriche introdotte da Fourier nello stesso decennio. Purtroppo, fallì nel tentativo di risolvere i casi più complessi. Fu Gustav R. Kirchhoff che sviluppò la prima teoria completa della piastra infessa. Egli ottenne la medesima equazione di Navier riuscendo, però, a esprimere tutte le condizioni al contorno in funzione dello spostamento trasversale e delle sue derivate rispetto a x e a y. Uno dei suoi contributi più significativi fu l’introduzione del metodo degli spostamenti virtuali per la risoluzione di vari problemi riguardanti le piastre. Kirchhoff espose il suo lavoro in un lungo articolo del 1850. L’equazione a cui pervenne fu la seguente:

a cui andavano aggiunte le opportune condizioni al contorno. Ad esempio, per una piastra con i lati fissati, le condizioni al contorno sono:

L’equazione dedotta da Kirchhoff mostrò che le figure ottenute da Chladni su una piastra quadrata corrispondono alle coppie autovalori-autofunzioni dell’operatore biarmonico con condizioni di bordo libero. Per coloro che si stanno chiedendo cosa coglia dire quanto detto fin qui, bhè, posso provare a semplificare la cosa in questo modo: durante la vibrazione della piastra vi sono dei punti che restano fermi. Se disponiamo della sabbia sulla piastra e la facciamo vibrare, i granuli si addenseranno in tali punti fermi così da formare le figure di Chaldni. Se immaginiamo di tagliare la piastra con piani ad essa paralleli otteniamo varie curve di livello, come mostrato nella figura sottostante, dove sono riportati alcuni grafici che ho ottenuto risolvendo l’equazione con Matlab.
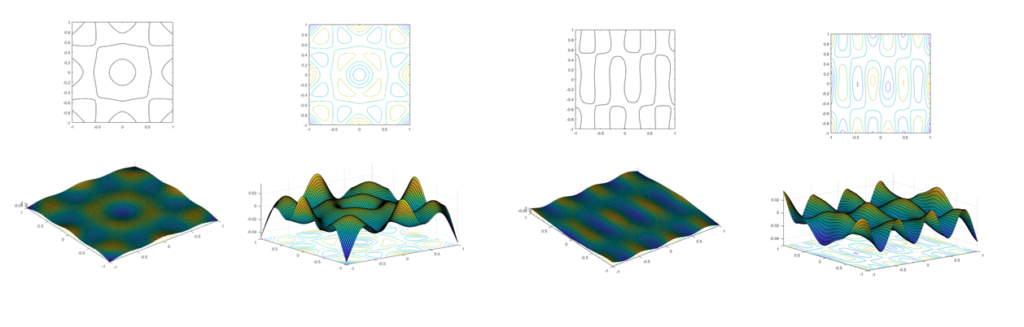
Nella prima figura in alto a sinistra vi è la figura riportata da Chladni; nella seconda in alto a destra varie curve di livello di colore diverso, nella sinistra in basso la deformata tridimensionale, nella figura in basso a destra una deformazione estremamente accentuata della figura precedente. Ritorniamo a Kirchhoff.
Egli provò a risolvere il problema delle figure di Chladni su una piastra circolare, la cui simmetria semplificava il problema e le soluzioni ma non riuscì comunque a trovare la soluzione completa. All’inizio del XX secolo l’esperto di teoria del suono John William Strutt, terzo barone di Rayleigh, riassunse la situazione nel suo monumentale trattato: The problem of a rectangular plate, whose edge are free, is one of great difficulty, and has for the most part resisted attack. Fu solo grazie a Walter Ritz, e al metodo da lui elaborato, che, nel 1909, si arrivò al primo calcolo corretto delle figure di Chladni su una piastra quadrata.
Al giorno d’oggi l’analisi delle piastre vibranti riveste un ruolo fondamentale in molte applicazioni, ed essa non può essere appresa senza conoscere la sottostante teoria della piastra. Le piastre sono dei componenti strutturali diritti, piani, in cui una dimensione, lo spessore, è molto più piccola delle altre. Esse, in realtà, non vengono utilizzate soltanto come componenti strutturali ma anche per completare le strutture (si pensi ai ponti lastricati). Dal punto di vista statico possono essere legate a una struttura con varie tipologie di vincolo (incastrate, appoggiate . . .). I carichi statici e dinamici che vi agiscono sopra sono applicati soprattutto perpendicolarmente alla sua superficie. Essi inducono nella piastra uno stato di sforzo interno, principalmente flessione, torsione e taglio. L’azione strutturale bidimensionale delle piastre fa si che le strutture risultino più leggere e ciò comporta notevoli vantaggi economici. Inoltre, numerose configurazioni strutturali richiedono una parziale o completa chiusura e ciò può essere ottenuto facilmente con tali componenti, eliminando coperture addizionali e risparmiando, quindi, sui materiali e sui costi di lavoro. Conseguentemente, al comportamento delle piastre, e delle strutture piane, è stata data particolare importanza nel corso degli anni. In ambito ingegneristico, molti componenti strutturali possono essere assimilati a lastre piane. Ad esempio, nell’ambito dell’ingegneria civile ci sono pavimenti e lastre di fondazione, porte di chiusura, pareti sottili, i rivestimenti e le lastricature dei ponti. Sono indispensabili anche nella costruzione navale e nell’industria aerospaziale. Le ali e una grande parte della fusoliera consistono di una piastra sottile con una serie di elementi longitudinali rigidi. Lo scafo di una nave, il suo ponte e la sua sovrastruttura sono ulteriori esempi di strutture a piastra rigide. Le piastre sono, inoltre, parti di macchinari o di altri dispositivi meccanici.
Di seguito un link di un video youtube in cui vengono generate le figure di Chladni: https://www.youtube.com/watch?v=wvJAgrUBF4w&t=36s


