Il retroscena
Il calcolo infinitesimale nacque e si sviluppò nel corso del XVII secolo. L’ispirazione per la sua invenzione venne da due direzioni: dalla matematica pura e dalla fisica. In matematica, il calcolo differenziale si sviluppò a partire dai metodi per trovare la tangente a una curva mentre il calcolo integrale si sviluppò a partire dai metodi per calcolare l’area delle figure piane e il volume dei solidi. In fisica, invece, si radicava sempre più la convinzione che la natura presentasse modelli regolari, molti dei quali implicavano qualche velocità di variazione. Di conseguenza, il calcolo infinitesimale fu il risultato di una serie di ricerche apparentemente disconnesse ma che rivelarono in realtà un’omogeneità di fondo.
Concetti e procedure importanti furono sviluppati da Fermat, Descartes e Barrow, ma le loro metodologie si limitavano a problemi particolari. Era necessario determinare un metodo generale.
a problemi particolari. Era necessario determinare un metodo generale.
Tra le discipline a cui ci si interessò particolarmente nel XVII secolo va annoverata sicuramente l’ottica con tutto ciò che le concerneva: ad esempio, le osservazioni astronomiche necessitavano di sistemi ottici precisi, attendibili, di cui si conoscessero le caratteristiche. Per studiare il passaggio della luce attraverso una lente era necessario, infatti, conoscere l’angolo secondo cui il raggio colpiva la superficie della lente, per poi poter applicare la legge di rifrazione. L’angolo che interessava era quello formato dal raggio luminoso e la normale alla curva. Poiché la normale a una curva si definisce attraverso la retta tangente, il problema si riconduceva alla ricerca di quest’ultima.
La necessità di definire la tangente ad una curva si riscontrava anche nello studio dei moti: la direzione del moto di un corpo coincide, in ciascun punto della sua traiettoria, con la tangente alla traiettoria nel punto.
Nel 1634 il francese Gilles Personne de Roberval, nel suo Traité des indivisibles, presentò un metodo per determinare le tangenti che generalizzava le riflessioni compiute nell’antichità da Archimede per trovare la tangente alla spirale che da lui prende il nome. Roberval, riprendendo le osservazioni di Galileo Galilei sul moto di un proiettile, arrivò a una definizione di tangente che risultava basata su concetti fisici, oltre che geometrici.
Pierre Fermat propose, nel manoscritto Methodus ad Disquirendam Maximam et Minimam, un metodo diverso per la determinazione della tangente a una curva che sembrava essere un’applicazione del suo metodo per i massimi, sebbene il francese a quel tempo non sapeva ben dire qual era la quantità che stava massimizzando.
Il problema di trovare aree di superfici, lunghezze di curve e volumi di solidi aveva anch’esso ovvie implicazioni di natura pratica (si pensi alla semplice esigenza di misurare campi o lunghezze in generale).
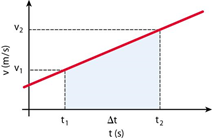
Galileo nei Discorsi e dimostrazioni matematiche intorno a due nuove scienze si occupò della questione da un punto di vista prettamente fisico, analizzando il grafico della velocità di un corpo in moto uniformemente accelerato in funzione del tempo: lo scienziato pisano si accorse infatti che l’area del triangolo sottostante la retta della velocità doveva rappresentare la distanza percorsa dal corpo nel tempo considerato.
Il ragionamento di Galilei fu ripreso e sviluppato in un metodo puramente geometrico da un discepolo dello scienziato toscano, Bonaventura Cavalieri, nell’opera Geometria Indivisibilibus Continuorum Nova quadam Ratione Promota. Il metodo degli indivisibili di Cavalieri si basava proprio sul principio di considerare l’area di una superficie come unione di infiniti segmenti paralleli, gli indivisibili dell’area, considerati come elementi infinitamente piccoli di area. Analoga trattazione avevano i volumi. Il termine usato da Cavalieri, indivisibile, potrebbe tradursi con l’espressione moderna di figura geometrica di spessore infinitesimo. Il matematico, inoltre, pare aver riconosciuto che il numero degli indivisibili all’interno di un’area dovesse essere infinito, ma non sembra aver elaborato concettualmente il problema.
Anche Fermat, ovviamente, lavorava ai problemi di calcolo delle aree e dei volumi. Già nel 1629 riuscì a trovare un modo per calcolare l’area sotto curve del tipo .
Newton, Leibniz e la nascita del calcolo infinitesimale
Newton and Leibniz, apparentemente in modo indipendente, elaborarono delle procedure algoritmiche che erano applicabili universalmente e rappresentavano le basi dei successivi concetti di derivata ed integrale. Lo sviluppo geometrico condusse Newton al metodo delle flussioni, mentre Leibniz sviluppò il calcolo differenziale.
All’inizio degli anni 1665-1666 Newton affermava di essere in possesso del metodo delle flussioni nel De analysi per aequationes numero terminorum infinitas.
Questa monografia, che v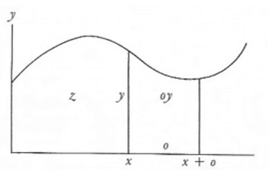 enne pubblicata nel 1711, fu inizialmente diffusa solo tra i suoi amici. All’interno del testo, l’inglese non fece un uso esplicito di tale metodo, né tantomeno ne esplicitò l’idea. Ciò che era presente nel testo era l’applicazione del concetto di infinitamente piccolo sia dal punto di vista geometrico sia dal punto di vista analitico. Newton sviluppò l’idea di un rettangolo (o momento) di area indefinitamente piccola e invece di determinare le quadrature come limite di una somma, determinò il tasso di cambiamento dell’area considerando l’incremento dei momenti in un dato punto.In tal modo determinò l’area stessa con ciò che noi oggi definiremmo integrale indefinito, ossia la funzione che definisce le ordinate. Il passo fondamentale è stato determinare la velocità di variazione: è come se dicessimo che la derivazione è presa come l’idea di base e l’integrale è definito in termini di questa.
enne pubblicata nel 1711, fu inizialmente diffusa solo tra i suoi amici. All’interno del testo, l’inglese non fece un uso esplicito di tale metodo, né tantomeno ne esplicitò l’idea. Ciò che era presente nel testo era l’applicazione del concetto di infinitamente piccolo sia dal punto di vista geometrico sia dal punto di vista analitico. Newton sviluppò l’idea di un rettangolo (o momento) di area indefinitamente piccola e invece di determinare le quadrature come limite di una somma, determinò il tasso di cambiamento dell’area considerando l’incremento dei momenti in un dato punto.In tal modo determinò l’area stessa con ciò che noi oggi definiremmo integrale indefinito, ossia la funzione che definisce le ordinate. Il passo fondamentale è stato determinare la velocità di variazione: è come se dicessimo che la derivazione è presa come l’idea di base e l’integrale è definito in termini di questa.
Ciò che Newton ha veramente fatto, quindi, è stato facilitare l’operazione piuttosto che chiarirne i concetti. D’altronde egli stesso affermava che: il suo metodo è una breve spiegazione piuttosto che un’accurata dimostrazione.
L’idea che egli aveva in mente era questa: l’ordinata y sembra rappresentare la velocità di incremento dell’area mentre l’ascissa rappresenta il tempo. Ora, il prodotto dell’ordinata per un piccolo intervallo della base restituisce una piccola porzione dell’area e l’area totale sotto la curva è semplicemente la somma di tutti questi momenti di area. Questo è esattamente il concetto di infinitesimo che compare nelle dimostrazioni di Galileo e Descartes delle leggi di caduta dei corpi, con la differenza che Newton riuscì a calcolare l’area dalla conoscenza della sua velocità di variazione in un singolo punto.
Le sue idee sul calcolo infinitesimale furono esposte nel Methodus Fluxionum et Serierum Infinitarum in cui più estesa esposizione del metodo. In questo libro Newton considerava le variabili coinvolte nel calcolo come quantità dinamiche generate dal moto continuo di punti, linee e piani piuttosto che come un aggregato di elementi infinitesimi, punto di vista che invece utilizzava nel De analysi. La velocità di variazione era chiamata flussione e indicata con una lettera avente sopra un punto; la quantità generata era chiamata fluente. Così se i fluenti sono x e y, le loro flussioni sono .
Newton stabilì, così, il problema fondamentale del calcolo: date certe quantità determinare la relazione tra le loro flussioni e viceversa.
Iniziavano ad essere chiaramente presenti gli elementi della derivazione: l’utilizzo della funzione di una sola variabile, la formulazione di un rapporto tra la variazione della variabile indipendente e la variazione della funzione; la determinazione del limite di questo rapporto quando il tasso di variazione tende a zero.
Nel frattempo anche Leibniz stava lavorando a problemi simili e così, il 24 ottobre 1676, Newton decise di inviargli una lettera in cui, in forma di anagramma, gli poneva il problema fondamentale del calcolo: dati i fluenti determinare le flussioni e viceversa.
Leibniz, come Newton, stava sviluppando le regole e il simbolismo per riunire tutte le considerazioni sugli infinitesimi in un’unica procedura algoritmica. Il matematico tedesco, tra le altre cose, stava lavorando al problema delle tangenti, così come a quello delle quadrature, e aveva raggiunto una soluzione basata sul triangolo caratteristico. E’ difficile dire quali siano stati gli eventi che lo portarono all’invenzione del calcolo differenziale, ma, come egli stesso scrisse successivamente, l’ispirazione per la sua applicazione del triangolo differenziale a una figura, va ricercata nella lettura del Traité des sinus du quart de cercle di Pascal.  Durante la lettura di questo testo, Leibniz capì che la determinazione della tangente a una curva dipendeva dal rapporto tra la differenza delle ordinate e la differenza delle ascisse quando queste diventavano infinitamente piccole; la quadratura, invece, dipendeva dalla somma delle ordinate per intervalli infinitesimi delle ascisse. Inoltre, le operazioni di somma e differenza erano le inverse le une delle altre. Di fatto anche Barrow era giunto a realizzare qualcosa del genere ma senza sviluppare il tutto in una procedura unificata.
Durante la lettura di questo testo, Leibniz capì che la determinazione della tangente a una curva dipendeva dal rapporto tra la differenza delle ordinate e la differenza delle ascisse quando queste diventavano infinitamente piccole; la quadratura, invece, dipendeva dalla somma delle ordinate per intervalli infinitesimi delle ascisse. Inoltre, le operazioni di somma e differenza erano le inverse le une delle altre. Di fatto anche Barrow era giunto a realizzare qualcosa del genere ma senza sviluppare il tutto in una procedura unificata.
Il triangolo armonico e il triangolo di Pascal sono strettamente relazionati. In particolar modo, in questi triangoli somme e differenze sono le inverse le une delle altre, proprio come il problema delle tangenti, dipendente dalla differenza delle ordinate, è l’inverso del problema delle quadrature, che dipende dalla somma di tutte le ordinate. Tuttavia, mentre nei triangoli le somme e le differenze sono finite, quelle tra le ordinate di una curva sono infinitesime e le formule “ordinarie” non sono, quindi, applicabili. Leibniz fu così costretto a sviluppare un metodo per determinare la somma e la differenza tra infinitesimi. Egli utilizzò dapprima la notazione e poi
per la somma (si noti che il simbolo di integrale altro non è che una S allungata) che chiamò integrale di x su consiglio dei fratelli Bernoulli. Per le differenze nel valore x utilizzò dx poiché trovare la differenza implicava una diminuzione della dimensione della quantità. Con queste notazioni Il matematico determinò le differenze delle somme, dei prodotti, dei quozienti etc.
Leibniz espose tali risultati in un’opera del 1684 intitolata Nova methodus pro maximis et minimis, itemque tangentibus ,qua nec irrationales quantitates moratur. Due anni più tardi, sugli Acta Eruditorum, il matematico tedesco pubblicò una spiegazione del calcolo integrale, nella quale le quadrature venivano presentate come casi particolari del metodo inverso delle tangenti.
Poiché la somma e la differenza sono evidentemente operazioni inverse l’una dell’altra, ne segue immediatamente che invertendo la differenziazione si ottengono le quadrature
La differenziazione assume, dunque, la posizione centrale nell’elaborazione leibniziana, attraverso la quale le quantità evanescenti fanno il loro ingresso in geometria. Secondario è, invece, il ruolo delle quadrature vedendo l’integrazione come il processo inverso della differenziazione.
Mentre Newton definiva il fluente come la quantità generata da una data flussione, che è la quantità avente una data grandezza come sua flussione, Leibniz definì l’integrale come la somma di tutti i valori di una grandezza, o come la somma di un numero infinito di rettangolo infinitamente sottili. Questi due punti di vista sono persistiti all’interno del calcolo, in cui ci sono due tipi di integrali: gli integrali indefiniti e gli integrali definiti. Ai primi ci si riferiva come “integrali di Newton”, ai secondi come “integrali di Leibniz”.
Quando venne pubblicato il primo libro sul calcolo infinitesimale nel 1711, non furono pochi gli oppositori ai metodi proposti da Newton. Questi, e in particolare il vescovo George Berkley nel suo libro del 1734 The analyst, a Discourse Addressed to an Infidel Mathematician, sottolineavano come fosse illogico dividere il numeratore e il denominatore per o se poi si pone o pari a 0. La risposta di Newton fu che egli non aveva mai posto o uguale a zero: aveva, invece, studiato cosa succedeva quando o si avvicinava
a zero senza mai assumerne il valore. Il metodo, infatti, riguardava le flussioni, non i numeri.
Ci volle più di un secolo per trovare una valida risposta alle obiezioni sollevate da Berkley, con la definizione rigorosa del concetto di “passaggio al limite”. Intanto, però, nonostante ci fossero delle lacune dal punto di vista logico, il metodo di newton si diffuse: era troppo utile per poter essere accantonato a causa di una serie di “cavilli” logici. Berkley era infuriato. Riteneva che il metodo funzionasse soltanto perché c’era una serie di errori che si annullavano a vicenda. Ma se si annullavano sempre forse non erano dei veri e propri errori.
Con il passare del tempo, con l’acquisizione di rigore logico, il calcolo infinitesimale divenne sempre più importante e, come è ovvio, iniziò ad essere rivendicato. Quando Leibniz pubblicò il suo lavoro nel 1864, alcuni degli amici di Newton si offesero e lo accusarono di avergli rubato le idee. I matematici continentali, soprattutto i Bernoulli, presero invece le parti di Leibniz accusando di plagio Newton. In effetti, come dimostrano gli scritti inediti, i due avevano raggiunto le loro scoperte in modo del tutto indipendente e quindi le accuse sarebbero potute cadere facilmente da entrambe le parti. Così non fu e la disputa infervorò: Johann Bernoulli estese la sua avversione da Newton all’intera nazione inglese, che vide così disastrata la propria matematica. Infatti, in Inghilterra i matematici rimasero fedeli alla concezione geometrica di Newton, che era difficile da usare. Gli analisti continentali, invece, adottando i metodi algebrici di Leibniz, portarono avanti l’argomento molto velocemente e così, la maggior parte dei risultati in fisica matematica si dovette a francesi, tedeschi, svizzeri e olandesi.


