Oggi ascoltavo mio fratello che ripeteva filosofia e a un certo punto ho avuto un pò da ridire su alcune cose scritte sul libro di testo. Non a livello filosofico, sia chiaro…il pensiero di Zenone (è di lui che si parla, come deducibile dal titolo) va apprezzato e contestualizzato. Ho avuto da ridire su concetti matematici (posti come commento al paradosso) scritti su un libro di filosofia moderno e ho, allora, pensato di scrivere questo articoletto.
Il paradosso di Achille e la tartaruga è uno dei più famosi paradossi del filosofo Zenone di Elea. Esso ci è pervenuto attraverso la descrizione che ne da Aristotele nella Fisica:
“Il secondo argomento è quello detto di Achille. Eccolo: il più lento corridore non sarà mai raggiunto nella sua corsa dal più veloce. Infatti sarà necessario che l’inseguitore proceda fin là donde si è mosso il fuggitivo, quindi è necessario che il corridore più lento si trovi sempre un pò più innanzi.”
Possiamo esprimere il paradosso in questo modo: Achille decide di sfidare una tartaruga in una gara di velocità. Consapevole, forse, dell’imparità della sfida decide di dare alla tartaruga un pò di vantaggio. Nel momento in cui la corsa ha inizio, Achille fa un passo avanti, andando a occupare la posizione in cui la tartaruga si trovava inizialmente. Quest’ultima, nel frattempo, ha infatti compiuto un passetto spostandosi in avanti. Assumendo che l’istante di partenza sia , possiamo riferirci a questo nuovo momento come al tempo
.
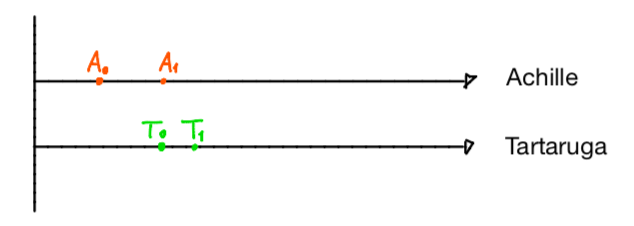
Achille e la tartaruga fanno, allora, un altro passo cosicchè la tartaruga si porta un pò più avanti e Achille va ad occupare la posizione che occupava prima la tartaruga. Siamo così giunti all’istante che chiamiamo .
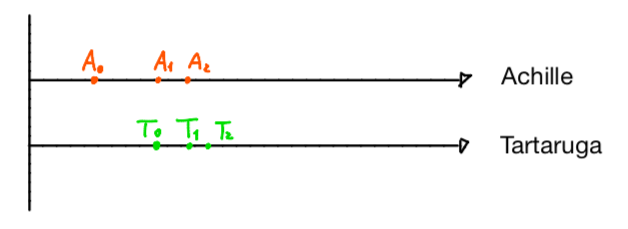
Proseguendo il ragionamento ci accorgiamo che Achille non raggiungerà mai la tartaruga e l’averle dato quel vantaggio iniziale ha predeterminato l’esito della gara.
Bene…tale ragionamento è inconsistente non solo da un punto di vista meramente pratico ma anche da un punto di vista squisitamente matematico. Ciò che voleva fare Zenone era dimostrare che se si assumeva l’infinita suddivisibilità dello spazio e del tempo il movimento diventava impossibile.
Dal paradosso, infatti, sembra apparire chiaro che per quanto potremmo aspettare un lungo tempo T, se spazio e tempo sono infinitamente divisibili, la somma di infiniti istanti (quelli impiegati da Achille per compiere i suoi balzi) sarà un numero infinito e quindi non vedremo mai Achille superare la tartaruga.
Ciò che è sbagliato in questo ragionamento è il pensare che la somma di infiniti termini debba per forza dare un numero infinito. In matematica esiste, infatti, il concetto di somma di una serie che estende il concetto di “somma di un numero finito di addendi”. Non ne parlerò, state tranquilli, sappiate solo che esistono le serie e le loro somme.
Vediamo come le serie ci permettono di risolvere il paradosso di Zenone.
Supponiamo che la tartaruga si muova a una velocità costante e che Achille abbia una velocità 10 volte maggiore di questa. La velocità di Achille diventa
. Indichiamo con
il vantaggio iniziale concesso da Achille.
Quando la gara inizia, il tempo che impiega Achille a passare dalla posizione alla posizione
è calcolabile come il rapporto tra lo spazio percorso e la velocità:
.
Nel tempo la tartaruga percorre lo spazio:
.
Al tempo Achille possiede uno svantaggio pari a
.
Per passare da a
, percorrendo quindi la distanza
, Achille impiega un tempo pari a:
.
In tale tempo la tartaruga passa da a
percorrendo lo spazio:
.
Reiterando il procedimento si ha che Achille percorre la distanza in un tempo:
e la tartaruga, in tale tempo, percorre:
.
Al passo si ha:
;
.
Achille raggiungerà la tartaruga se la somma di tutti i tempi impiegati a percorrere i successivi svantaggi converge a un tempo finito, cioè se la serie
converge. Tale serie può essere riscritta come:
.
Achille impiega, dunque, un tempo pari a per raggiungere la tartaruga.
[jupdf-viewer file= https://www.gquadroblog.com/wp-content/uploads/2018/09/Achille-e-la-tartaruga.pdf width=800px height=600px]


