Il “movimento” atomico: la struttura dell’atomo attraverso i secoli – Parte IV

L’introduzione della quantistica: l’atomo di Bohr

Al quadro delle particelle se n’era aggiunta una nuova grazie ai risultati ottenuti da Planck e Einstein: il fotone, che interagiva con l’elettrone scambiandovi energia a passi quantizzati.

L’interazione tra materia (atomi) ed energia (fotoni) fu sintetizzata da Einstein nella formula nota .

Nel 1913 il fisico danese Niels Bohr, utilizzando i risultati della teoria quantistica, perfezionò il modello di Rutherford aggiungendogli alcune delle basi teoriche che gli mancavano. Poiché gli elettroni nel loro moto non irradiavano necessariamente energia, ipotizzò che esistessero alcuni stati in cui l’elettrone potesse muoversi senza emettere energia, mantenendo quindi costante la somma di energia cinetica e energia potenziale. Tali stati vennero definiti stazionari. Affinché l’energia dell’elettrone si mantenesse costante doveva verificarsi che il valore del suo momento angolare durante la descrizione dell’orbita fosse un multiplo di   : il momento angolare era stato dunque quantizzato. Il fatto che il momento angolare potesse assumere solo alcuni valori veniva espresso mediante la relazione

dove

• n = 1, 2, 3, . . . ;
• m = massa dell’elettrone;
• v = velocità dell’elettrone;
• h = costante di Planck;
• r = raggio dell’orbita circolare.

Bohr applicò la sua modellizzazione all’atomo di idrogeno, costituito da un unico elettrone ruotante attorno al nucleo. Uguagliando il valore della forza coulombiana, che attirava l’elettrone verso il nucleo, al valore della forza centrifuga diretta lungo il raggio e volta verso l’esterno, fu possibile ricavare l’espressione del raggio dell’orbita:

la quale mostrava che anche il raggio era quantizzato, cioè anche il raggio poteva assumere solo determinati valori.

L’elettrone che orbitava intorno al nucleo possedeva un’energia cinetica   dovuta al movimento, e un’energia potenziale  , dovuta alla posizione dell’elettrone nel campo elettrostatico del nucleo. La somma delle due energie costituiva l’energia totale   che, con opportune manipolazioni matematiche, era data da

.

Tale formula esprimeva la quantizzazione dell’energia dell’atomo di idrogeno. Se si forniva energia a un elettrone che si trovava sullo stato stazionario caratterizzato da n=1, l’elettrone la assorbiva solo se essa era sufficiente a farlo passare ad uno stato stazionario successivo. L’elettrone eccitato sarebbe poi tornato naturalmente nello stato a energia minore (n=1), riemettendo energia sottoforma di radiazione. Nel passare da una stato caratterizzato da   a uno stato caratterizzato da  , l’energia emanata avrebbe avuto una frequenza data da   

La stessa relazione poteva essere scritta utilizzando i numeri d’onda (ossia il numero di lunghezze d’onda contenute in 1 cm, dati da  , con c = velocità della luce):

,

dove  R era la costante di Rydberg.

Con tali formule era possibile calcolare tutte le frequenze a cui l’atomo di idrogeno poteva emettere o assorbire per il passaggio dell’elettrone tra gli stati stazionari di numeri quantici   e  .

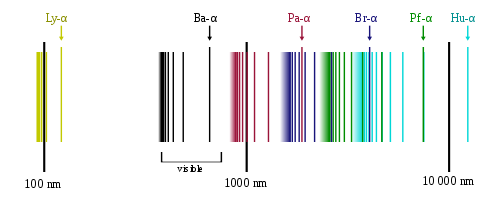
Quando si eccitava dell’idrogeno nel suo stato fondamentale (n = 1), il numero di atomi eccitati era elevatissimo e i vari elettroni passavano su livelli diversi: alcuni su quelli aventi n=2, altri su quelli aventi n=3, e così via.Tornando verso lo stato fondamentale gli elettroni percorrevano spazi diversi e quindi emettevano a frequenze diverse. Tali frequenze, nel loro insieme, costituivano lo spettro dell’atomo di idrogeno.