Esercizio Saint – Venant

Pubblicato da Giuseppe Gentile il

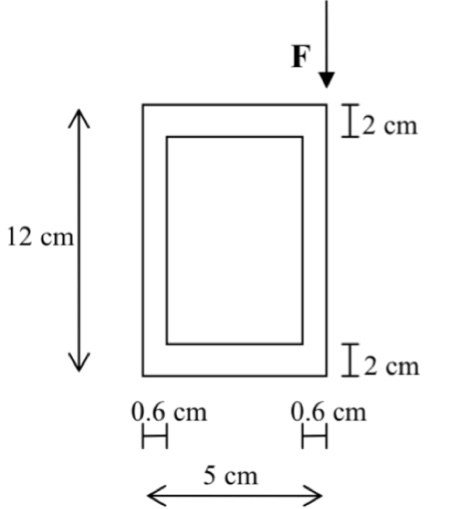
Si consideri la sezione rettangolare cava indicata in figura:

  1. Determinare il momento torcente agente sulla sezione.
  2. Calcolare il valore medio della tensione tangenziale dovuta al momento torcente e disegnare il flusso delle tensioni.
  3. Considerando un materiale di modulo elastico G=800000 \frac{kg}{cm^2}, calcolare l’angolo unitario di torsione.

Svolgimento 

Individuo il centro di taglio della sezione:

Poichè la forza di taglio F non passa per il centro di taglio, la sezione è soggetta anche a torsione.

Separo il problema di taglio dal problema di torsione:

Il momento torcente agente sulla sezione vale M_3=-F \cdot 2,5= - 500 kg cm.

calcolo la tensione tangenziale dovuta al momento torcente utilizzando la formula di Bredt:

Calcolo il valore di \tau_{3i} nei vari tratti:

Riporto in figura l’andamento delle tensioni tangenziali.

Calcoliamo l’angolo unitario di torsione \Theta.

Per tanti altri esercizi svolti seguitemi sul mio profilo Instagram: @gquadroblogesercizi

Categorie: Esercizi di Scienza delle CostruzioniEsercizi sul problema di Saint-Venant
Tag:

Articoli correlati

Esercizi Strutture Iperstatiche

Struttura Iperstatica

Negli appunti che seguono viene risolta una struttura iperstatica con il teorema dei lavori virtuali. I vincoli presenti sono incastro e glifo (o pattino).  La sollecitazione è costituita da due carichi distribuiti.

Esercizi Strutture Iperstatiche

Struttura Iperstatica

Negli appunti che seguono viene risolta una struttura iperstatica con il teorema dei lavori virtuali. I vincoli presenti sono cerniere. La sollecitazione è costituita da tre carichi distribuiti.

Esercizi Strutture Iperstatiche

Struttura Iperstatica

Negli appunti che seguono viene risolta una struttura iperstatica con il teorema dei lavori virtuali. I vincoli presenti sono cerniera e carrello.  La sollecitazione è costituita da due carichi distribuiti e un carico concentrato.