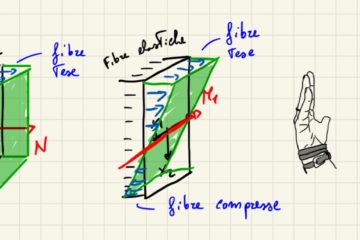
Teoria pragmatica per svolgere gli esercizi sul problema di Saint Venant – Forza Normale

Pubblicato da Giuseppe Gentile il

  • Forza Normale sulla sezione
  • Scomposizione dei movimenti
  • Analisi dei movimenti
  • Traslazione
  • Rotazione intorno all’asse orizzontale
  • Rotazione intorno all’asse verticale
  • Formula di Navier
  • Asse neutro
  • Determinazione grafica posizione asse neutro
  • Determinazione grafica posizione asse neutro
  • Diagramma delle tensioni assiali
  • Asse di sollecitazione
  • Asse di flessione
Categorie: Teoria Scienza delle Costruzioni
Tag:

Lascia un commento

Il tuo indirizzo email non sarà pubblicato. I campi obbligatori sono contrassegnati *

Articoli correlati

La meccanica del continuo

Il campo di trasporto: cos’è e quali informazioni contiene

Consideriamo un corpo in una configurazione di riferimento . A seguito di un processo deformativo il corpo assume la configurazione attuale . Il punto P della configurazione di riferimento diviene allora il punto P’ della Leggi tutto…

Teoria Scienza delle Costruzioni

Teoria pragmatica per svolgere gli esercizi sul problema di Saint Venant – Flessione

Teoria pratica per svolgere gli esercizi di Saint Venant inerenti la flessione. Viene spiegato il significato fenomenologico della formula e in seguito si ottengono le componenti del vettore curvatura.

Teoria Scienza delle Costruzioni

Teoria pragmatica per svolgere gli esercizi sul problema di Saint Venant – Introduzione

Saint Venant: introduzione. Negli appunti è spiegato il procedimento con cui si passa dallo stato di sollecitazione agente su una trave allo stato di sollecitazione a cui è sottoposta una sua sezione interna. Individuate le azioni interne, le si relazionano con le corrispondenti tensioni e si spiega quindi qual è lo scopo pratico del problema di Saint Venant.