Studiare la seguente funzione:

* Non è richiesto lo studio della derivata II.
1) Dominio
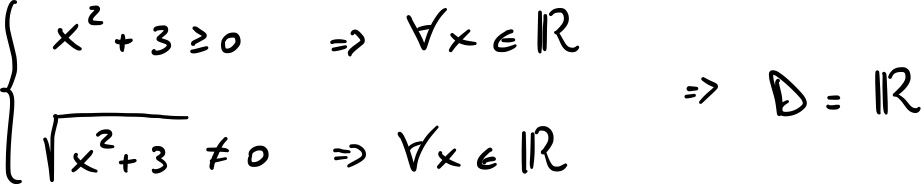
2) Parità e disparità
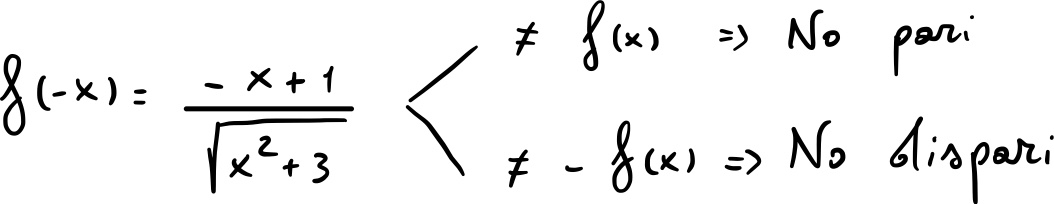
3) Intersezioni con gli assi
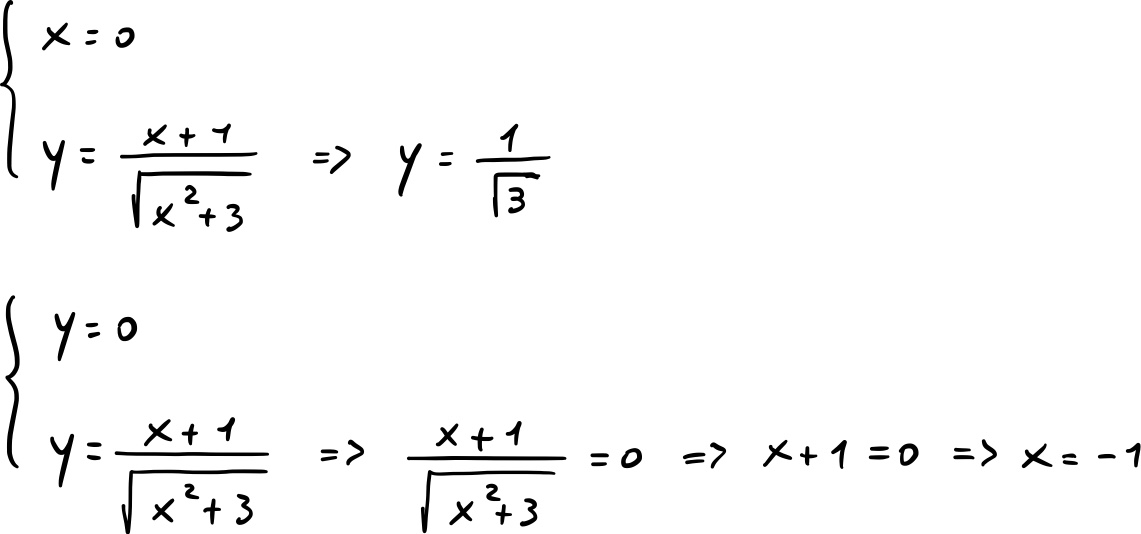
4) Studio del segno
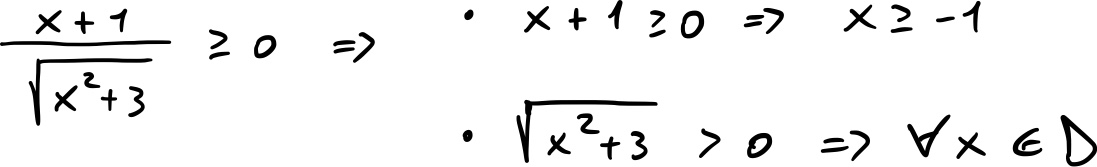
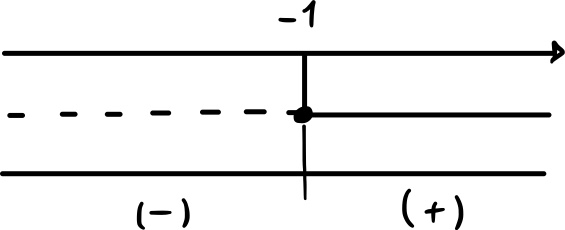
Con le informazioni ottenute possiamo tracciare il seguente schema:
5) Limiti
Non essendo presenti punti di discontinuità, la funzione non presenta asintoti verticali.
Cerchiamo eventuali asintoti orizzontali.

La retta è asintoto orizzontale per
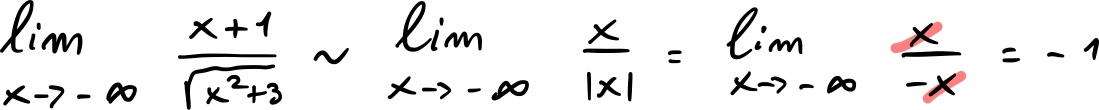
La retta è asintoto orizzontale per
Aggiorniamo lo schema con le nuove informazioni:
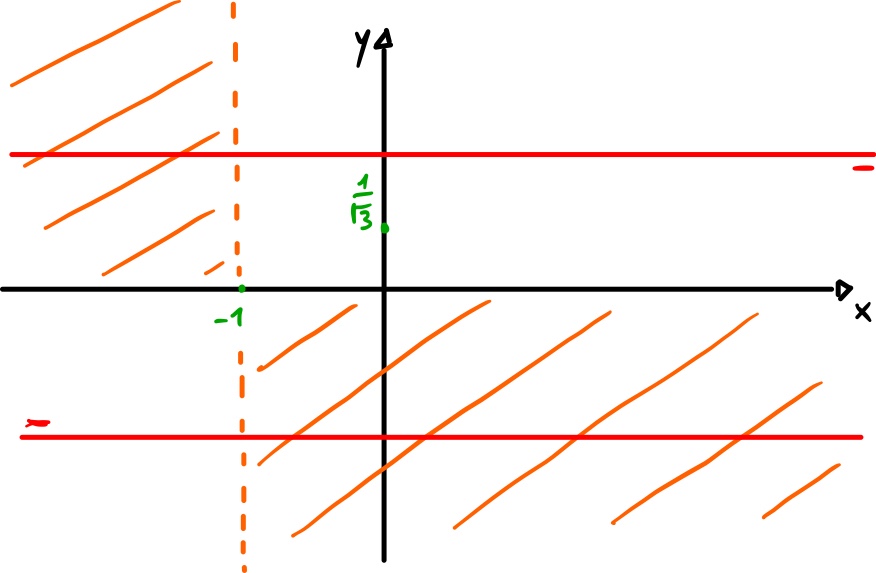
6) Derivata I e relativo studio
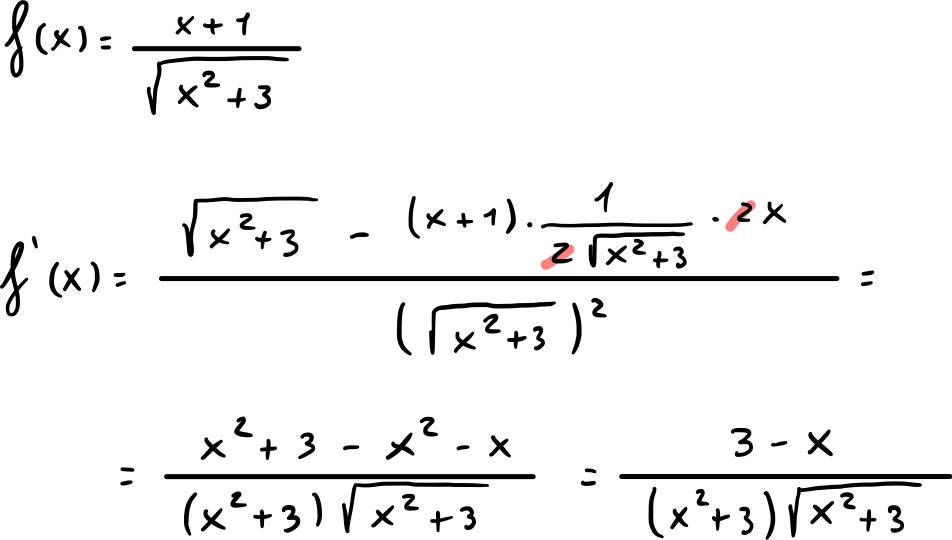
Studio il segno della derivata I:
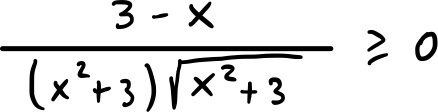
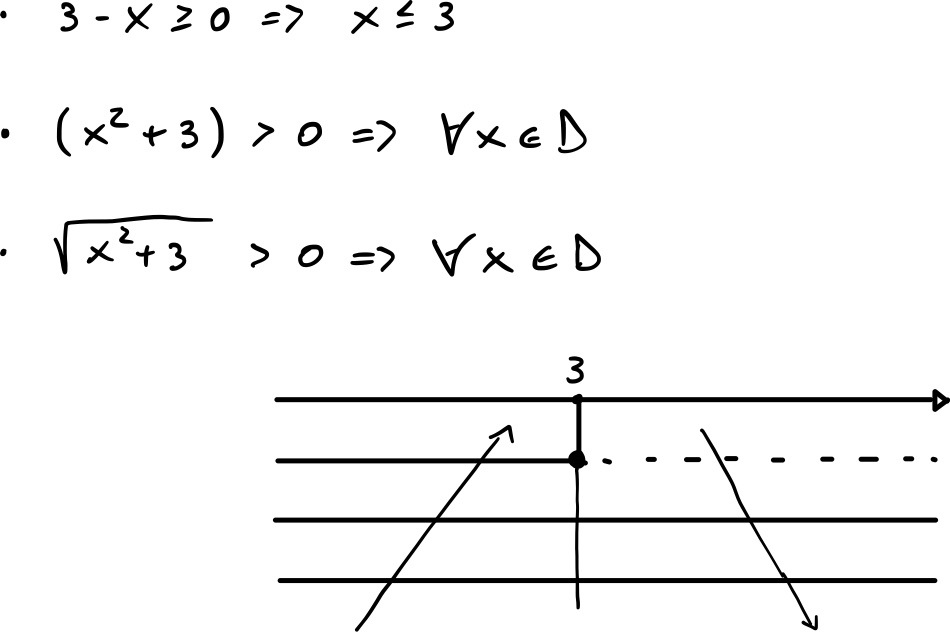
è punto di massimo relativo.
Il massimo relativo è dato da:
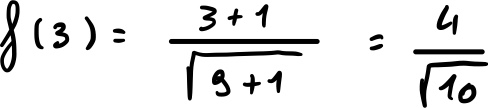
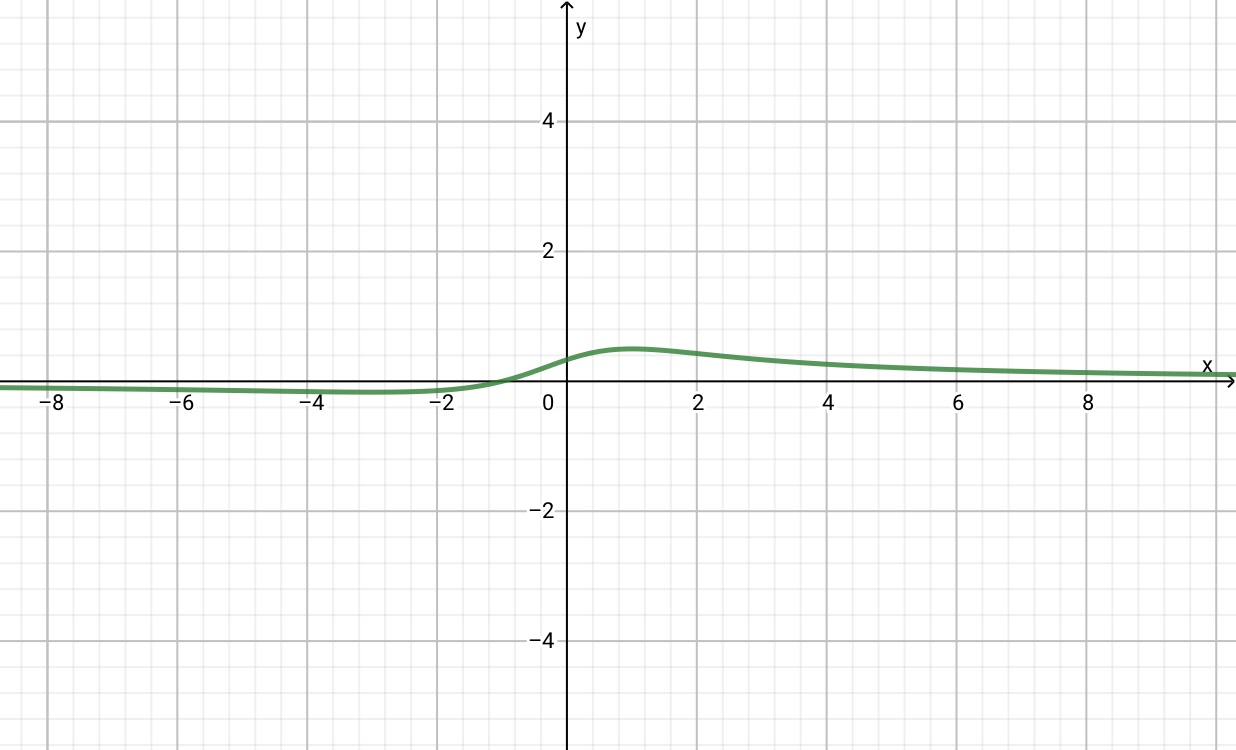
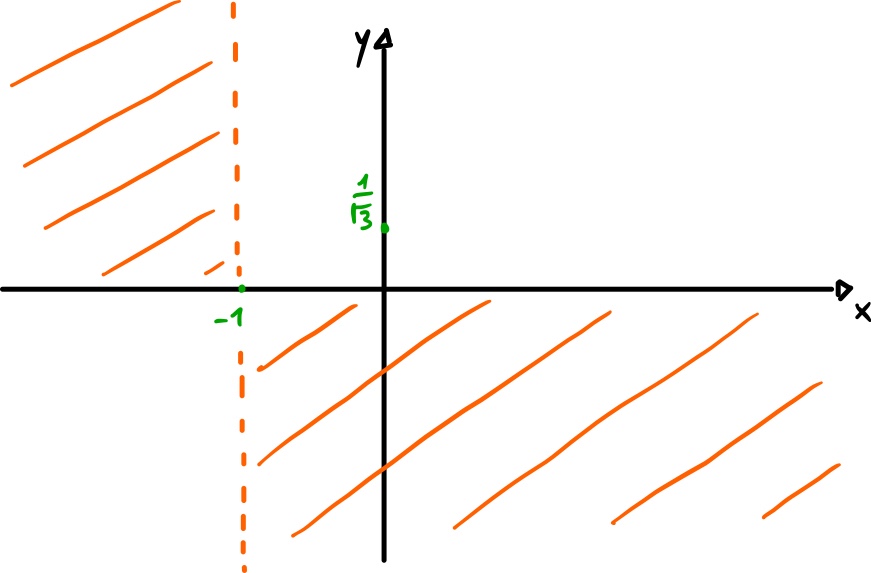
7) Grafico qualitativo
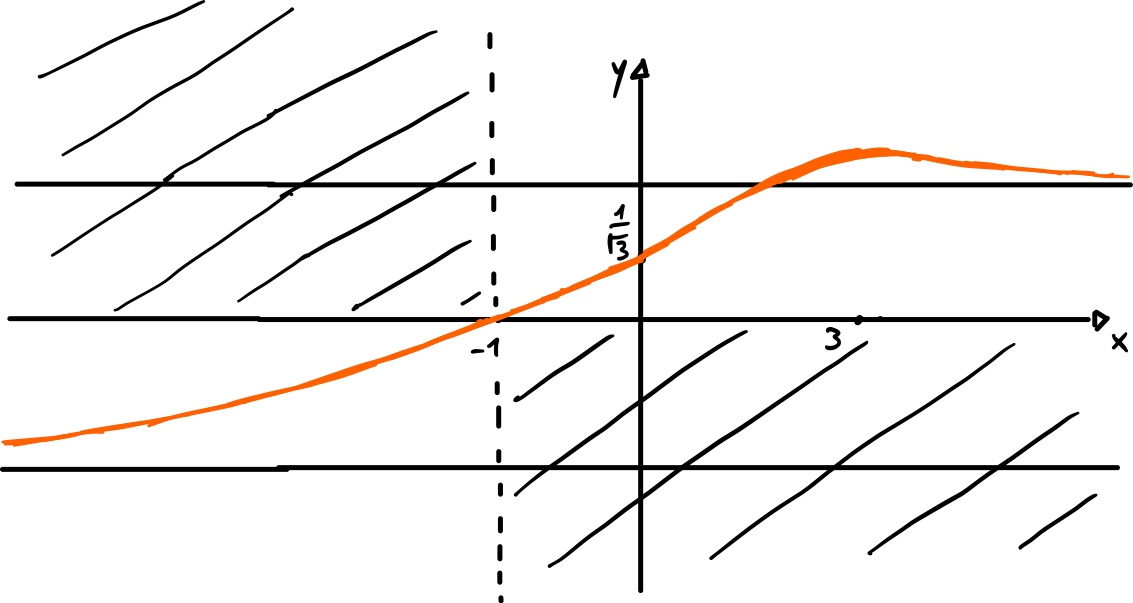
Il grafico esatto (ottenuto con l’ausilio del calcolatore) è il seguente: